2

Yes, there are many methods to find the equation; the easiest being the process of solving the eqn. of circle putting the three points. But what I didn't understand is the another method which my book describes as:

If three points be $A$ , $B$ , $C$ , then write $S$ = equation of circle on $AB$ as diameter. $P$ = equation of line through $A$, $B$ .

The required equation of the circle is $$ S + \lambda . P = 0$$ , where $\lambda$ is found by passing it through the point $C$ .

What did the book do here?? Why should the circle have $AB$ as diameter and how does the equation represent the circle passing through $A , B , C$ ? It chose a circle having $AB$ as diameter. But the circles passing through these three points can have any diameter. So, why $AB$? How can the equation be the equation of the required circles?

3 Answers3

1

You can see by plugging in the points that this equation is true on the points $A$, $B$, and $C$. By completing the square we can also show that it is the equation for a circle. The method works because there is a unique circle passing through $A$, $B$, and $C$.

Matt Samuel
  • 58,164
1

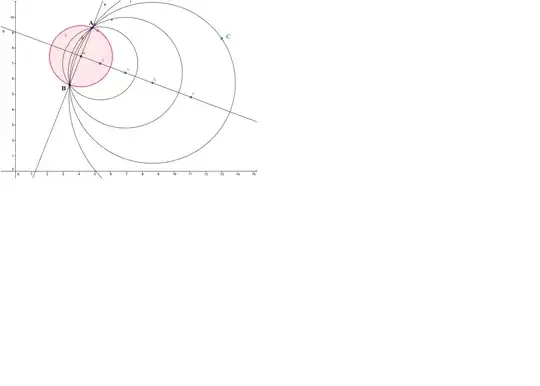
How can the equation be the equation of the required circles???

It described the family of circles passing through $A$ and $B$, and then picked the appropriate element from that family.

If you have a point $(X,Y)$ on a circle with center $(x,y)$ and radius $r$, its equation is

$$r^2=(X-x)^2+(Y-y)^2=X^2-2Xx+x^2+Y^2-2Yy+y^2$$

which is of the form $(X^2+Y^2)+aX+bY+c=0$ with $a=-2x,b=-2y,c=x^2+y^2-r^2$. So as long as $4c<a^2+b^2$ you can always turn an equation of this form back into a circle.

The equation of a line, on the other hand, is something like $dX+eY+f=0$. So if you combine them to $S+\lambda P=0$ you get

$$(X^2+Y^2)+(a+\lambda d)X+(b+\lambda e)Y+(c+\lambda f)=0$$

which again has the form of a circle equation. And since each individual term of the sum was zero for $A$ and $B$, their sum must be zero there as well. So you know that this will always be a circle through $A$ and $B$. And since you know it contains two real points, you don't have to worry about the $4c<a^2+b^2$ condition I wrote above, since if that were violated you'd have zero or imaginary radius, and couldn't have two real points located on the circle.

Why should the circle have AB as diameter

It doesn't really matter what circle you start with. You could take any circle passing through $A$ and $B$, although a different choice would lead to a different value of $\lambda$. But the one with the diameter is easiest to compute.

As a variant, you can play the same game with two different circles passing through $A$ and $B$, and do $S_1+\lambda S_2=0$. Then you'd get an equation which starts with $(1+\lambda)(X^2+Y^2)$ but since you could as well divide the whole resulting equation by $(1+\lambda)$ it would still be a circle. (Except if $\lambda=-1$, then you'd have a line instead, so that happens if $A,B,C$ are collinear.) The only problem is that if $C$ already lies on $S_2$, you'd get a division by zero. To avoid that you could write $\lambda S_1+\mu S_2=0$, and you could compute these as e.g. $\lambda = S_2(C)$ and $\mu = -S_1(C)$ to ensure that $C$ satisfies the combined equation.

MvG
  • 42,596
0

The topic is called “family of lines”.

enter image description here

It says, from A and B, form (using two-point form) P, the equation of AB.

It also says, form (using A and B as endpoints of diameter) S, the equation of the red circle. [There is a simple formula for doing that too.]

For different values of λ, S + λP = 0 represents a family of circles passing through A and B.

For a specific value of λ, that equation will be the circle that passes through C.

The co-ordinates of C can be used to determine that value of λ. Hence, the equation of the circle passing through A, B, C is known.

Mick
  • 17,141