I am looking for a proof of a problem as follows:
Let six points $A_1, A_2, A_3, A_4, A_5, A_6$ lie on a circle. Define $C(A,B)$ be any circle through points $A, B$. Let $C(A_i,A_{i+1}) \cap C(A_{i+3}, A_{i+4}) = B_i, B_{i+3}$ we take modulo 6. Let $B_1, B_2, B_3, B_4, B_5$ lie on a circle $(C)$. Let $C(A_i,A_{i+1}) \cap C(A_{i+1}, A_{i+2}) = C_{i+1}$. Show that $B_6$ also lie on the circle $(C)$ and six points $C_1, C_2, C_3, C_4, C_5, C_6$ lie on a circle.
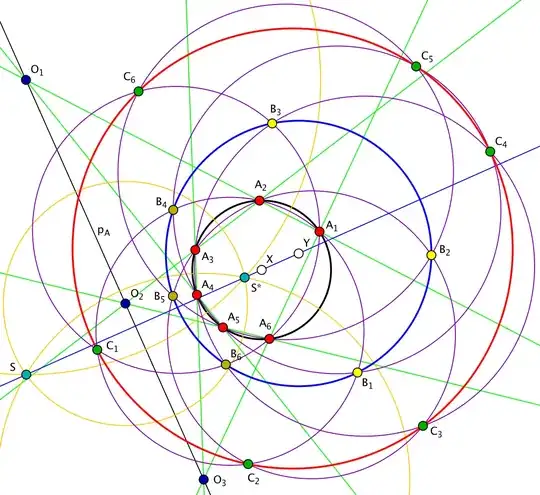
By Pascal's theorem the three intersection points $$O_1 = A_1A_2 \cap A_4A_5 \, , \,\,\, O_2 = A_2A_3 \cap A_5A_6 \, , \,\,\, O_3 = A_3A_4 \cap A_6A_1$$ lie on a common line (the Pascal's line) $p_A$. Draw the three circles $k_1\,, \,\, k_2\,,\,\, k_3$ centered at the points $O_1,\,O_2\,O_3$ respectively and each of them orthogonal to the circle $k_A$ (the circle passing through the points $A_1, A_2, A_3, A_4, A_5, A_6$). Then, $k_1, k_2, k_3$ intersect at two common points $S$ and $S^*$, i.e. the circles $k_1, k_2, k_3$ are coaxial (have a common radical axis, passing through the points $S$ and $S^*$, and orthogonal to the Pascal line $p_A$).
From now on, by $k(ABC)$ I denote the unique circle (or a straight line) passing through the points $A, B, C$.
Lemma 1. Let $k_B$ be a circle different from $k_A$. Take an arbitrary point $B_1$ from $k_B$ and draw the pair of circles $k(B_1A_1A_2)$ and $k(B_1A_4A_5)$. Then the second intersection point $B_4 (\neq B_1)$ of $k(B_1A_1A_2)$ and $k(B_1A_4A_5)$ also lies on $k_B$ if and only if $k_B$ orthogonal to circle $k_1$.
Proof: By construction of circle $k_1$, if one performs an inversion with respect to $k_1$, then $A_1$ is mapped to $A_2$ and $A_4$ is mapped to $A_5$. Thus, circle $k(B_1A_1A_2)$ is mapped to itself and is therefore orthogonal to $k_1$. Analogously, circles $k(B_1A_4A_5)$ is also orthogonal to $k_1$. By the radical axis theorem applied to the circles $k_A, \, k(B_1A_1A_2)$ and $k(B_1A_4A_5)$, the three radical axes $B_1B_2, \, A_1A_2$ and $A_4A_5$ intersect at a common point, which is $O_1 = A_1A_2 \cap A_4A_5$ -- the center of circle $k_1$. Therefore, point $B_1$ is mapped to $B_4$ under the inversion with respect to circle $k_1$. Consequently, if $k_B$ is orthogonal to $k_1$, since $B_1 \in k_B$ its inversive image $B_4$ also lies on $k_B$. Conversely, if both $B_1$ and $B_4$ lie on $k_B$, then the circle $k_B$ is orthogonal to $k_1$.
Lemma 2. Let $B_1$ and $B_2$ be two different points in the plane. Let the pair of circles $k(B_1A_1A_2)$ and $k(B_1A_4A_5)$ intersect again at the second point $B_4 (\neq B_1)$, and let the pair of circles $k(B_2A_2A_3)$ and $k(B_2A_5A_6)$ intersect again at the second point $B_5 (\neq B_2)$. Then the four points $B_1, B_2, B_4, B_5$ lie on a common circle $k_B$ if and only if $k_B$ is orthogonal to the three circles $k_1, k_2, k_3$.
Proof: Let $k_B$ be a circle passing through points $B_1$ and $B_2$. By Lemma 1, points $B_4$ and $B_5$ also lie on $k_B$ if and only if $k_B$ is orthogonal to both circles $k_1$ and $k_2$. Therefore, the radical axis $SS^*$ of $k_1$ and $k_2$ passes through the center of $k_B$ whenever $k_B$ is orthogonal to $k_1$ and $k_2$. However, by construction, $SS^*$ is a common radical axis for all three circles $k_1, \, k_2$ and $k_3$ which means that $k_B$ is orthogonal to $k_3$ as well.
Corollary 3. In the setting of Lemma 2, let the four points $B_1, B_2, B_4, B_5$ lie on a common circle $k_B$. If $B_3$ is another (arbitrary) point on $k_B$, then the second intersection point $B_6$ of the pair of circles $k(B_3A_3A_4)$ and $k(B_3A_6A_1)$ also lies on $k_B$.
Proof: Follows directly from Lemma 2.
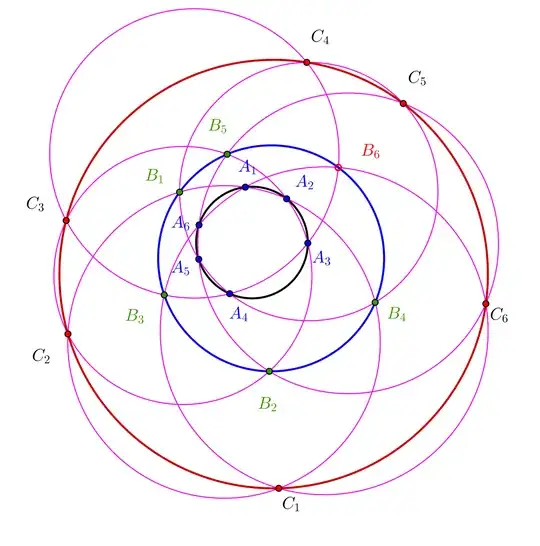
From now on, I am in the setting of Lemma 2, Corollary 3 and the statement of the original problem, where points $A_1, A_2, A_3, A_4, A_5, A_6$ lie on the circle $k_A$ and the points $B_1, B_2, B_3, B_4, B_5, B_6$ lie on the circle $k_B$. In the notations of the original problem $C(A_6,A_1)$ is the circle $k(B_3A_6A_1)$, the circle $C(A_1,A_2)$ is the circle $k(B_1A_1A_2)$, the circle $C(A_5,A_6)$ is the circle $k(B_2A_5A_6)$ etc.
Lemma 4. The four lines $B_1B_4,\, B_2B_5,\, A_2C_2$ and $A_5C_5$ intersect in a common point $D$.
Proof: Define $D$ as the intersection point of the lines $B_1B_4$ and $B_2B_5$. Let us look at the three circles $k_B, \, C(A_1A_2)$ and $C(A_2,A_3)$, where $C_2$ is the second point of intersection of $C(A_1A_2)$ and $C(A_2,A_3)$, the one that is different from $A_2$. Then their three corresponding radical axes $B_1B_4,\, B_2B_5$ and $A_2C_2$ intersect at the common point $D$. Analogously, the three circles $k_B, \, C(A_4A_5)$ and $C(A_5,A_6)$ define the three radical axes $B_1B_4, \, B_2B_5$ and $A_5C_5$ which intersect at the common point $D$.
Lemma 5. The four points $A_2, A_5, C_2, C_5$ lie on a common circle $k_{25}$.
Proof: As a consequence of Lemma 4, the two chords $B_1B_4$ and $A_2C_2$ of the circle $C(A_1,A_2)$ satisfy $$B_1D \cdot DB_4 = A_2D \cdot DC_2.$$ Similarly, again by Lemma 4, the two chords $B_1B_4$ and $A_5C_5$ of the circle $C(A_4,A_5)$ satisfy $$B_1D \cdot DB_4 = A_5D \cdot DC_5.$$ Consequently $$ A_2D \cdot DC_2 = B_1D \cdot DB_4 = A_5D \cdot DC_5$$ which is possible if and only if the four points $A_2, A_5, C_2$ and $C_5$ lie on the the same circle, we call $k_{25}$.
Lemma 6. The four points $C_5, \, C_6, \, C_1$ and $C_2$ lie on a common circle, we call $(C)$.
Proof: It follows from Lemma 5 and Miquel's theorem applied to the circles $C(A_5,A_6), \, C(A_6,A_1), \, C(A_1, A_2), \, k_{25}$ and $k_{A}$.
Finally, we can apply Lemmas 5 and 6 consecutively first to points $A_3, \, A_6, \, C_3, \, C_6$ and second to points $A_1, \, A_4, \, C_1, \, C_4$ in order to show that first the points $C_6, \, C_1, \, C_2$ and $C_3$ lie on a common circle, which has to be again $(C)$ and second that the points $C_1, \, C_2, \, C_3$ and $C_4$ also lie on a common circle, which is $(C)$.
I like coordinates. The incidence relations you are interested in are invariant under Möbius transformations, so a natural setup for this problem would be the one-point compactification of the plane. Think $\mathbb{CP}^1$ if you want to, but I'll not use complex numbers for coordinates in this answer. Since your setup is invariant under Möbius transformations, you can choose specific coordinates of three points without loss of generality. So I'll choose $A_1$ to be the point at infinity, and fixed coordinates on the $x$ axis for two other points. Thus the “circle” through all the $A_i$ is the $x$ axis in my setup, and I can use parameters for the $x$ coordinates of the remaining points.
$$A_1=\infty\quad A_2=(a,0)\quad A_3=(0,0)\quad A_4=(b,0)\quad A_5=(1,0)\quad A_6=(c,0)$$
I created an interactive illustration of this specific version of your configuration, where you can move the points around and see the configuration change accordingly. I alternated between fixed and variable points in an attempt to make things more symmetric, in the hope of making individual expressions not too complicated.
Next we can pick an arbitrary point $B_1=(d,e)$ anywhere in the plane. This results in the
$$B_4=\frac1{(a-d)^2+e^2}\begin{pmatrix} (a(b-d)+(a-b))(a-d)+ae^2 \\ (a-b)(a-1)e \end{pmatrix}$$
computed as the second point of intersection between the corresponding circles.
Choosing $B_2=(x,y)$ will define the circle through $B_1,B_2,B_4$. On the other hand this allows us to construct $B_5$ as the intersection of $C(A_2,A_3)$ and $C(A_5,A_6)$. We can and check whether that point lies on the same circle. In general it does not. The condition for $B_1,B_2,B_4,B_5$ to be cocircular can be factored into the following independent conditions:
$$ a=1 \\\vee\\ (d-a)^2+e^2=(1-a)(b-a) \\\vee\\ (a-c-1)(x^2+y^2) + 2cx = ac \\\vee\\ (a-c)e(x^2+y^2) + (-ab + bc - a + b)ex\\ + ((a-c)((b-d)d - e^2) - (a-b)(c-d))y + (a-b)ce=0 $$
The first three of these conditions can be seen as non-degeneracy constraints. If $a=1$ then $A_2=A_5$, which is a degenerate situation. The second condition characterizes the situations where $B_1$ and $B_4$ would coincide, while the third is when $B_2$ and $B_5$ would be the same. So if we can assume that all points in the configuration are distinct, then we can concentrate on the last condition.
It describes a circle, so we now know that the point $B_2$ must lie on a certain circle if $B_5$ is to be cocircular with $B_1,B_2,B_4$. Actually this circle already passes through $B_1$ and $B_4$. So knowing all the $A_i$ and $B_1$ already fixes the circle on which all the $B_i$ must lie.
We can play the same game for $B_3$ and $B_6$ instead of $B_2$ and $B_5$. What's the conditions for $B_1,B_3,B_4,B_6$ being cocircular if we choose $B_3=(x',y')$?
$$ (d-a)^2+e^2=(1-a)(b-a) \\\vee\\ (x'-c)^2+y'^2=(c-b)c \\\vee\\ (a-c)e(x'^2+y'^2) + (-ab + bc - a + b)ex'\\ + ((a-c)((b-d)d - e^2) - (a-b)(c-d))y' + (a-b)ce=0 $$
The last conditon is the same as above, so if the cocircularity condition is satisfied for $B_1,B_2,B_4,B_5$ and all points are distinct, and if $B_3$ is chosen from that same circle, too, then the cocircularity condition must be satisfied for $B_1,B_3,B_4,B_6$ as well, and all six $B_i$ are cocircular.
A similar game can be played for the $C_i$ as well. Their coordinates are considerably more complicated, though, and so are the conditions for cocircularity of four of these. But assuming the $B_i$ to be cocircular (i.e. assuming the respective last condition to hold for $B_2$ and $B_3$), one can demonstrate that all the points must be cocircular, too. In particular, if the condition for $B_2$ holds, then one can show that $(C_1,C_2,C_5,C_6)$ and $(C_2,C_3,C_4,C_5)$ are cocircular, and if the condition for $B_3$ holds, then $(C_1,C_2,C_3,C_4)$ and $(C_1,C_4,C_5,C_6)$ are cocircular. If both hold, then all points must be cocircular. You could start by defining the circle via $C_1,C_2,C_3$, then add $C_4$ due to $(C_1,C_2,C_3,C_4)$, add $C_5$ due to $(C_2,C_3,C_4,C_5)$ and add $C_6$ due to $(C_1,C_4,C_5,C_6)$. All again assuming distinct points, of course.
I computed the things I described above with a lot of help from Sage. I included the full log of my Sage session, including descriptions, in the blog post I created for the interactive illustration.
This is an idea I had, but it doesn't seem to work as I had hoped.
Here is one approach, building on the help of computer algebra and programming. Four points $A,B,C,D$ in the complex plane (or its one-point compactification) are cocircular iff their cross ratio is real:
$$\frac{(A-C)(B-D)}{(A-D)(B-C)}\in\mathbb R\;.$$
Now you can translate both the cocircularities you assume and the ones you want to prove into fractions of this kind. If you find a way to multiply fractions from known cocircularities in such a way that most terms cancel out and you are left with a fraction of one of the unknown cocircularities, then you have a proof, as the product of real numbers will be a real number again. But how do you find such a way to multiply terms?
Think about this in a logarithmic way. The fraction above can be written as $$(A-C)^{x_{AC}}(B-D)^{x_{BD}}(A-D)^{x_{AD}}(B-C)^{x_{BC}}\\ \text{with}\quad x_{AC}=x_{BD}=1\quad\text{and}\quad x_{AD}=x_{BC}=-1\;.$$ Multiplying terms of this form means adding the corresponding values in the exponents. So you can think of this as a vector space: you have one dimension for each unordered pair of points, i.e. $\binom{6\cdot 3}{2}=153$ dimensions. You have up to $\binom{6}{4}=15$ known cocircularities for each of your circles, and you have essentially $3$ different vectors you can build from these, identifying vectors with their negatives. I let my CAS do this for me, and came up with a $153\times330$ matrix of rank $68$.
Now you can check whether one of the vectors for the cocircularities you want to prove is in the span of this matrix. Unfortunately that does not seem to be the case. Pity! Miquel's six circle theorem can be proven by this approach, and this one here does look a bit like an extended version of that one, so my hopes were high.
