For an ellipse with minor radius $b$, show that the product of distances from the foci to any tangent line is $b^2$

Question

Consider the ellipse with equation: $$\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$$ How do we prove the product of distances from the foci to any tangent line is $b^2$?

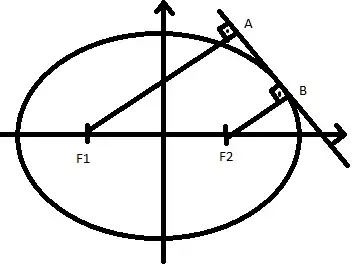
$$F_1A \cdot F_2B = b^2$$

Answer 1

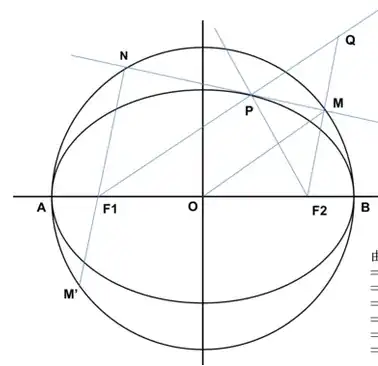
It is well know $$\angle QPM=\angle F_{2}PM,\Longrightarrow PQ=PF_{2},QM=F_{2}M$$ so $$OM//F_{1}Q\Longrightarrow OM=\dfrac{F_{1}Q}{2}=\dfrac{F_{1}P+F_{2}P}{2}=a$$ so $M,N\in\bigodot O$ so $F_{1}M'=F_{2}M$ so $$F_{1}N\cdot F_{2}M=F_{1}N\cdot F_{1}M'=F_{1}A\cdot F_{1}B=(a+c)(a-c)=b^2$$

Answer 2

Let' say that $A(x_0,y_0)$ is the point of intersection of the tangent $$\epsilon:\begin{array}[t]{l}\frac {x} {a^2} x_0+\frac y {b^2}y_0=1\\(b^2 x_0) x+(a^2 y_0)y -a^2b^2=0\end{array}$$ and the ellipse.

The distance between $F_1(-c,0)$ and $\epsilon$ is: $$d_1=\dfrac{\left|-c b^2 x_0-a^2b^2\right|}{\sqrt{b^4x_0^2+a^4y_0^2}}$$

Respectively, the distance between $F_2(c,0)$ and $\epsilon$ is: $$d_2=\dfrac{\left|c b^2 x_0-a^2b^2\right|}{\sqrt{b^4x_0^2+a^4y_0^2}}$$ Thus, we have:

$$d_1\cdot d_2\begin{array}[t]{l}=\cdots =\dfrac{\left|a^4b^4-b^4x_0^2c^2\right|}{b^4x_0^2+a^4y_0^2}=\dfrac{\left|a^4b^4-b^4x_0^2(a^2-b^2)\right|}{b^4x_0^2+a^4y_0^2}\\\\ \end{array}$$ However, from the initial equation of the ellipse, since $A(x_0,y_0)$ belongs to the ellipse, we can prove that: $$a^4b^4=a^2 b^4x_0^2+b^2a^4y_0^2$$ Making the substitution above, we have:

$$d_1\cdot d_2=\dfrac{\left|a^2 b^4x_0^2+b^2a^4y_0^2-b^4a^2x_0^2+b^6x_0^2\right|}{b^4x_0^2+a^4y_0^2}=\cdots=b^2$$

Answer 3

Some hints:

• Where are the foci located in terms of $a$ and $b$? You can either look it up, or use the definition of what an ellipse is to find them. (An ellipse is all points in a plane for which the sum of the distances from the two foci is a constant.)
• For a given point on the ellipse, what is the slope of the tangent? You'll use this to get an equation for the tangent, and from there you can get expressions for the perpendicular distance to the tangent from each focus.

Answer 4

WLONG, we can represent any point on the given Ellipse as $x=a\cos A,y=b\sin A$

So, the equation of the tangent at $(a\cos A,b\sin A)$ will be $\dfrac{x\cdot a\cos A}{a^2}+\dfrac{y\cdot b\sin A}{b^2}=1$

$$\iff bx\cos A+ay\sin A-ab=0$$

The coordinates of the foci are $(\pm ae,0)$ where $e$ is the eccentricity

So, the distances will be $$\frac{|\pm ae\cdot b\cos A-ab|}{\sqrt{(b\cos A)^2+(a\sin A)^2}}$$ and consequently their product will be

$$=a^2b^2\cdot\frac{(1-e\cos A)(1+e\cos A)}{(b\cos A)^2+(a\sin A)^2} =a^2b^2\cdot\frac{(1-e^2\cos^2A)}{a^2(1-e^2)\cos^2A+a^2\sin^2A}=b^2$$

as $b^2=(1-e^2)a^2$