It's well-known that point $P$ has an isogonal conjugate with respect to quadrilateral $ABCD$ if and only if projections $P$ onto sides $ABCD$ lie on the circle (and similar criteria for $n$-gon).
However, I don't know proof of this fact.
I saw a proof in Chapter 17 (page 209) in 高中数学竞赛解题策略 几何分册 by 沈文选 and 杨清桃.
My translation of the proof (with some modifications):
Property 7. If a polygon has a pair of isogonal conjugate points $P$ and $Q$, the projections of $P$ and $Q$ onto all sides of the polygon lie on a circle centered at the midpoint of $PQ$.
Proof.
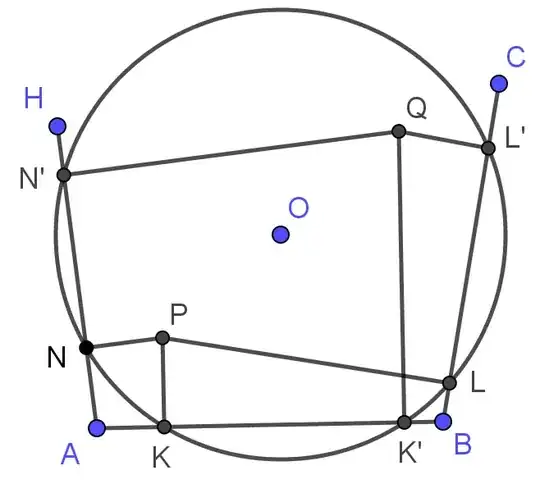
Let the projection of $P,Q$ on sides $AB,BC,\dots,HA$ be $K,K',L,L',\dots,N,N'$.
Since $\angle ANP=\angle AKP=90^\circ$, the points $A,K,N,P$ are concyclic, then
$$
\angle ANK=\angle APK=90^\circ-\angle PAK
$$
Similarly, $A,Q,N',K'$ are concyclic, then
$$
\angle AK'N'=\angle AQN'=90^\circ-\angle QAN'
$$
By definition of isogonal conjugate, $\angle PAK=\angle QAN'$, so $\angle ANK=\angle AK'N'$, so $N,N',K,K'$ lie on a circle, the center of this circle is the intersection of perpendicular bisectors of $NN',KK'$, which is the midpoint of $PQ$. By the same method, we can prove $K,K',L,L'$ lie on a circle centered at the midpoint of $PQ$, this circle and the previous circle have the same center and both pass through $K,K'$, so they are the same circle. Continuing in this way we can prove projections of $P,Q$ on all sides lie on the same circle.
Then the author claimed the converse is true, which is same as your criterion:
$P$ has an isogonal conjugate with respect to the polygon if and only if projections $P$ onto all sides lie on a circle.
The proof of the converse is omitted, but I think we can define $Q$ as the reflection point of $P$ about $O$ and deduce the projections of $Q$ lie on the same circle and deduce the isogonal property.

Another criterion for existence of isogonal conjugates:
Isogonal conjugate points are foci of an inscribed ellipse of the polygon.
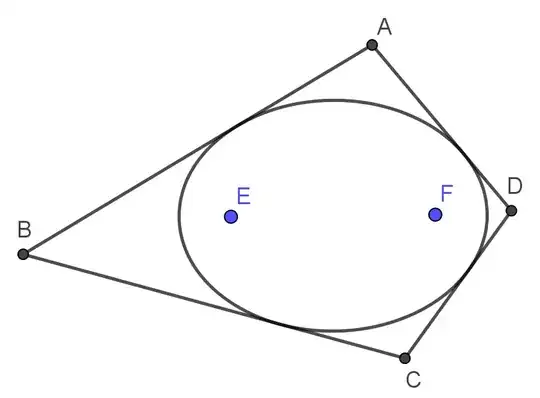
This "inscribed ellipse" criterion relates to your criterion by a property of ellipse: draw the perpendiculars from the foci to tangents, the feet of the perpendiculars lie on a circle, the major circle of the ellipse, also in
For an ellipse with minor radius $b$, show that the product of distances from the foci to any tangent line is $b^2$
How to prove that the foot of perpendicular drawn from a focus to any tangent of an ellipse lies on its auxiliary circle?
This "inscribed ellipse" criterion relates to the isogonal property by Equal angles formed by the tangent lines to an ellipse and the lines through the foci.


