32

I have been trying to think of a rather basic way of proving this, but it seems a bit elusive. In the case with boundary (looking at them as quotients in $ [0,1] \times [0,1] $), they can be distinguished from the connectedness of the boundary (thanks Stefan), but I'm interested in the open case (looking at them as quotients in $ [0,1] \times (0,1) $, i.e. as manifolds without boundary).

If there is not such basic way to do this, it would be interesting to read about some advanced methods you guys know about.

Stefan Hamcke
  • 27,733
Tom
  • 329
  • The boundary is the subset of points $x$ such that no neighborhood (within $M$) is homeomorphic to an open subset of $\Bbb R^2$. So in the cylinder $C=S^1\times I$ the boundary is $S^1\times{0,1}$. – Stefan Hamcke Feb 15 '15 at 17:01
  • Do homeomorphic spaces have homeomorphic bounduaries? – Tom Feb 15 '15 at 17:02
  • Yes. If $X$ and $Y$ are spaces such that $x\in X$ has a neighborhood $N$ with a homeomorphism $\phi:N\to\phi(N)$, where $\phi(N)$ is an open subset of $\Bbb R^2$, then if $f:X\to Y$ is a homeomorphism, $f(N)$ is such a neighborhood as well (One calls this a Euclidean neighborhood). – Stefan Hamcke Feb 15 '15 at 17:06
  • 1
    You are right. But what happens if we consider the open cylinder and Moebius band? – Tom Feb 15 '15 at 17:08
  • Do you mean the "open" Möbius band ? There should be a way to prove that the open cylinder and the open Möbius band are not homeomorphic, but I don't know an argument right now. – Stefan Hamcke Feb 15 '15 at 17:08
  • 12
    Any simple closed curve on the cylinder cut it into two pieces. Cutting a Möbius band along its middle give you a longer Möbius band. Kids love that! – achille hui Feb 15 '15 at 17:26
  • As far as the bounty description, "This is an interesting question. I prefer a rigorous-ish proof, similar to the example given in the post. (An arts and crafts activity wouldn't win the bounty.)", appears to exclude the above proof by @achille hui, it is based on a thoroughly misguided notion of mathematical rigour. – joriki Aug 15 '15 at 04:44
  • @joriki: Proving that every simple closed curve on the cylinder cuts it into two pieces is quite nontrivial, and is arguably far beyond the "basic" methods that the question expresses a preference for. – Eric Wofsey Aug 15 '15 at 05:12
  • 2
    @joriki I wouldn't say achille hui is misguided. It was just a comment. I just wanted to make it clear that it couldn't, by itself, be made a bounty-worthy answer. – Christopher King Aug 15 '15 at 05:43
  • @PyRulez: That seems to be a misunderstanding; I was trying to say that dismissing achille's answer as an "arts and crafts activity" was based on a misguided notion of rigour, not that achille is misguided. – joriki Aug 15 '15 at 06:25

7 Answers7

38

Here is the most elementary argument I can come up with. Let $C$ denote the open cylinder and $M$ denote the open Moebius band. Note that there exists a compact subset $K\subset C$ such that for any compact $K'$ such that $K\subseteq K'\subset C$, $C\setminus K'$ is disconnected (for instance, you can take $K$ to be the "equator" of $C$). On the other hand, I claim that no compact subset $K\subset M$ has this property. Indeed, let $K\subset M$ be compact; identifying $M$ as a quotient of $[0,1]\times(0,1)$ in the standard way, there is then some $\epsilon>0$ such that $K$ is contained in the image of $[0,1]\times[\epsilon,1-\epsilon]$ under the quotient map (for instance, because the images of sets of the form $[0, 1] \times (\epsilon, 1-\epsilon)$ are open and cover $K$). Let $K'$ be this image; then $K'$ is compact, $K\subseteq K'\subset M$, and $M\setminus K'$ is connected.

Eric Wofsey
  • 330,363
  • $\backslash$ means set-difference, not quotient, correct? – Christopher King Aug 15 '15 at 05:40
  • @PyRulez: Yes. Note that you should use \setminus and not \backslash, as otherwise the spacing around it will look wrong. – Eric Wofsey Aug 15 '15 at 05:44
  • 5
    This is charming. Morally it's exactly the same thing as the "cut down the middle..." argument, with none of the tricky details. –  Aug 16 '15 at 01:03
  • 4
    Nice. This looks to me like a proof that the open Möbius band has less than two ends (in the sense of Freudenthal), whereas the open cylinder has at least two. Is that a reasonable interpretation? – Niels J. Diepeveen Aug 16 '15 at 02:42
  • @NielsDiepeveen: Yes, that's exactly right. – Eric Wofsey Aug 16 '15 at 05:10
  • This is related to the definition of "ends" of a topological space. The open Möbius strip has one end, while the open cylinder has two. https://en.wikipedia.org/wiki/End_%28topology%29 – Cheerful Parsnip Aug 18 '15 at 15:42
  • @EricWofsey Thank you so much. Once I am new on this type of proof, could you please explain a little bit more why $M\setminus K'$ is coneccted? Thank you – Quiet_waters Jan 12 '21 at 17:21
  • 1
    @Quiet_waters: $[0,1]\times(0,\epsilon)$ and $[0,1]\times(1-\epsilon,1)$ are each connected, and their images in $M\setminus K'$ intersect since $(0,x)$ is identified with $(1,1-x)$ in $M$. – Eric Wofsey Jan 12 '21 at 19:49
  • @EricWofsey perfect, thank you so much. – Quiet_waters Jan 12 '21 at 21:10
10

One-point compactification of an open cylinder is homotopy equivalent to $S^2\vee S^1$; and one-point compactification of Moebius band is just $\mathbb RP^2$. One-point compactifications of homeomorphic spaces have to be homeomorphic too, but two obtained spaces have different $\pi_1$.

Andrey Ryabichev
  • 2,682
  • 13
  • 24
8

As with most questions where we want to keep from getting into deep arguements, it is a questions of how deep can we go? Here is what I came up with for a intuitive arguement:

First, we notice that we can embed (Put in so it doesn't really change) the cylinder $C$ into $\mathbb{R}^2$. Just think of sitting the cylinder on the table, putting your hands inside and pushing the sides down and out away from the center.

enter image description here

If the cylinder and Möbius strip were homeomoprhic, we could also embed it in the plane. But we cannot, and here is why:

Any map from the Möbius strip into the plane will not be injective, which means that (at least) two points will be sent to the same place, no matter what. Here is a Möbius strip, with the two sides identified.

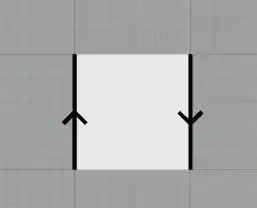
enter image description here

And here is the same Möbius strip with two circles that only intersect once in the Möbius strip. (This is the important part.)

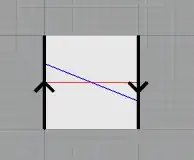
enter image description here

If we wanted to embed the Möbius strip, we would also embed the circles. So lets put the red circle in first, standardly, and the try to put in the blue circle.

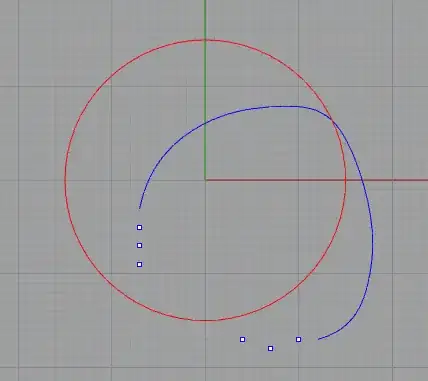
enter image description here

We can see that blue circle should be on both sides of the red circle, but for that to happen, they must intersect each other twice! So, we can't embed the Möbius strip into the plane, hence, the cylinder and the Möbius strip are not homeomorphic.

N. Owad
  • 6,822
  • Good answer. If I may ask, why should the blue circle be on both sides if the red, instead of tangent? – Christopher King Aug 18 '15 at 15:18
  • 1
    This actually is where it goes a little "deep." The blue cirle is transverse to the red - Together they form a basis for the tangent space. Which means it must cross and not just be tangent. Great question though, I was trying to keep it simple in my answer, but this is important. – N. Owad Aug 18 '15 at 15:24
  • Could I have a reference for this type of reasoning? It sounds cool. – Christopher King Aug 18 '15 at 15:27
  • 2
    This is a basic tool used in differential topology. There are a lot of good books, but the one I learned out of is this but try the wikipedia page first – N. Owad Aug 18 '15 at 15:30
  • @EricWofsey I am not sure I agree. All I really am using is that in the plane, two circles intersecting transverely must do so an even number of times. I don't think that requires the Jordan curve theorem. Does it? – N. Owad Aug 18 '15 at 15:57
  • Both the cylinder and the Mobius strip are "incomplete" in their embeddings (as all embeddings are...they don't show "all" the data). So in what sense can we embed the cylinder but not the Mobius strip? What is the criteria you are using to say something is embedded? – Cybernetic Feb 12 '23 at 17:46
6

An open-ended cylinder has the Jordan curve property - remove any subset homemorphic with a circle and you get a space which is not path connected. There is a circle you can remove from any Möbius strip which leaves the space connected.

Of course, the Jordan curve theorem is notoriously tricky and technical to prove, but at least it is intuitive what is going on.

Thomas Andrews
  • 177,126
  • 2
    (As a side note, because the cylinder is homeomorphic to $\mathbb R^2 \setminus {0}$, the JCT for the cylinder is immediately logically equivalent to the JCT for the plane.) –  Aug 16 '15 at 01:04
  • Oh, I definitely didn't mean that it was difficult to prove for the cylinder, given its truth on the plane, only that it is painful to prove for the plane from first principles. But if you can assume it for the plane, then yes, my answer here is probably the simplest approach. – Thomas Andrews Aug 18 '15 at 14:52
  • Agreed. The comment was mostly for the interested reader, rather than you. :) –  Aug 18 '15 at 14:53
1

The open Moebius band contains the closed Moebius band as a subspace, the cyclinder (or puncutred plane) does not. Though a rigorous justification of the latter may be a bit tricky.

Hagen von Eitzen
  • 374,180
1

Okay, I'm throwing my hat in the ring here. The cylinder is orientable while the Möbius band is not. It's easy to see that the Möbius band isn't, since you can find an explicit orientation reversing path. To show that the cylinder is orientable is slightly trickier, but is still easy since one has a method to define a consistent orientation across the entire cylinder. For example, thinking of the cylinder as embedded in space, take an outward pointing normal and use the right hand rule to induce an orientation of the cylinder.

Cheerful Parsnip
  • 27,278
  • I just saw John Mangual also mentioned orientability. I'll leave this since it gives some details on how to establish that one is orientable and the other isn't. – Cheerful Parsnip Aug 18 '15 at 16:26
-5

Let's be clear we have $X = [0,1]\times (0,1)$ with two different identification maps:

  • $f:(0,x) \in X \mapsto (1,x) \in X$ this gives a cylinder $Y$
  • $f:(0,x) \in X \mapsto (1,1-x) \in X$ this gives a Möbius band $Z$

Even though $Y$ and $Z$ are open, we can take their closure and $\partial \overline{Y} = S^1 \cup S^1$ while $\partial \overline{Z} = S^1 $. See Chapter 4 of the notes of Allen Hatcher on Point Set Topology for a discussion on quotient spaces.

#1 Consider the subspace $X_0= (0,1) \times [\frac{1}{4}, \frac{3}{4}]$ common to both spaces. Let $f:Y\to Z$ be a homeomorphism and the closure $\overline{X_0}\subset Y$ is a cylinder while $\overline{f(X_0)} \subset Z$ is a Mobius band.

#2 Cylinder is orientable. Mobius band isn't.

#3 Remove the meridian circle $ [0,1] \times \frac{1}{2} $ from a cylinder - it is not connected. Remove a meridian circle from a Möbius band, it remains connected. Jordan curve is not necessary, merely that if a continuous map $\phi:[0,1] \to \mathbb{R}$ has positive and negative values, then $\phi(x) = 0$ somewhere.

cactus314
  • 24,438
  • Not quite. The closure of the set of all points in a topological space is itself. It is in fact open and closed. – Christopher King Aug 15 '15 at 19:33
  • 3
    You have simply shown that there is no homeomorphism which respects the original space. This is not correct. – Christopher King Aug 15 '15 at 20:34
  • @PyRulez My constructions are fine. If the two spaces where homeomorphic, we could map one meridian circle to the other $S^1 \subset X \leftrightarrow S^1 \subset Y$. Since both spaces fiber over the circle, we can take a closed interval over each point in $S^1$. The result is a closed cylinder on the one hand and a closed Möbius band on the other. – cactus314 Aug 15 '15 at 21:09
  • 1
    Pu can't just take their closure - the quotients have closures, but they might not be unique. For example, the open interval has two compactifications. – Thomas Andrews Aug 16 '15 at 00:48
  • @ThomasAndrews sure I can; I am taking the closure of a subset of the cylinder/Mobius band in the relative topology. – cactus314 Aug 16 '15 at 01:15
  • 1
    @johnmangual Do you think the $\mathbb S^1\setminus {1}$ and $(0,1)$ are not homeomorphic? Because their closures in their natural containing spaces are not homeomorphic. The point is, you only have "containing spaces" because you've picked them. You don't have a natural container space in which to do the closure, and the closure can vary depending on how you embed them. Just consider the Open square in both the Mobius strip and cylinder - they have different closures, but they are homeomorphic. – Thomas Andrews Aug 16 '15 at 01:23
  • 2
    Your point #1 only shows that if there is a homeomorphism, it can't send that subset in one space to the same subset in the other space. – Thomas Andrews Aug 16 '15 at 01:30