Burgers' equation with piecewise linear initial data

Question

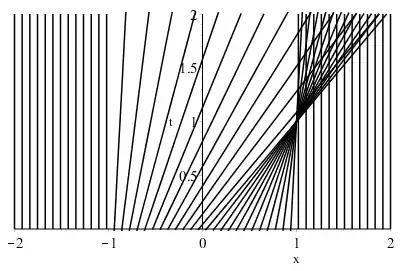
Solve $$ u_t + u u_x = 0 $$ with initial data $$ u(x,0) = g(x) = \left\lbrace \begin{aligned} &0 &&\text{for}\; x < -1\\ &1-|x| &&\text{for}\; {-1}\leqslant x \leqslant 1 \\ &0 &&\text{for}\; x > 1\, . \end{aligned} \right. $$ In what region is the solution single-valued? Confirm this observation by sketching or plotting the base characteristics.

$$\frac{dt}{d\tau }=1$$ $$t=\tau $$ $$t(\tau=0)=0$$

$$\frac{dx}{d\tau}=u$$ $$x=g(\xi)\tau+\xi$$ $$x(\tau=0)=\xi$$ $$\frac{du}{d\tau}=0$$ $$u=g{\xi}$$ $$u(\tau=0)=g(\xi)$$

How should I take my "solutions" further? Any help is appreciated

Answer 1

This problem is closely related to this one. The solution $u = g(x-ut)$ deduced from the method of characteristics is valid as long as it is single-valued, and we have $$ u(x,t) = \left\lbrace \begin{aligned} &0 &&\text{for}\; x < -1\\ &\tfrac{x+1}{t+1} &&\text{for}\; {-1}\leqslant x \leqslant t\\ &\tfrac{x-1}{t-1} &&\text{for}\; t\leqslant x \leqslant 1\\ &0 &&\text{for}\; x > 1 \end{aligned} \right. $$ Here, the solution is single-valued for times $t<t_b$, where $$ t_b = \frac{-1}{\inf g'} = 1 $$ is the breaking time. This time corresponds to the intersection of characteristic curves in the $x$-$t$ plane:

Answer 2

Follow the method in http://en.wikipedia.org/wiki/Method_of_characteristics#Example:

$\dfrac{dt}{ds}=1$ , letting $t(0)=0$ , we have $t=s$

$\dfrac{du}{ds}=0$ , letting $u(0)=u_0$ , we have $u=u_0$

$\dfrac{dx}{ds}=u=u_0$ , letting $x(0)=f(u_0)$ , we have $x=f(u_0)+u_0s=f(u)+ut$ , i.e. $u=F(x-ut)$

$u(x,0)=\begin{cases}0&\text{for}~x<-1\\1-|x|&\text{for}~-1\leq x\leq1\\0&\text{for}~x>1\end{cases}$ :

$\therefore u=\begin{cases}0&\text{for}~x-ut<-1\\1-|x-ut|&\text{for}~-1\leq x-ut\leq1\\0&\text{for}~x-ut>1\end{cases}$

$u(x,t)=\begin{cases}0&\text{for}~x<-1~\text{or}~x>1\\\dfrac{x+1}{t+1}&\text{for}~-1\leq\dfrac{x-t}{t+1}\leq1\\\dfrac{x-1}{t-1}&\text{for}~-1\leq\dfrac{t-x}{t-1}\leq1\end{cases}$