The problem is:
Consider Burgers' equation, $$u_t +uu_x = 0 $$ $$ u(x,0) = f(x) $$ where $$f(x) = \begin{cases} 1 - |x-2| &\mbox{if}\,\, 1\leq x \leq3, \\ 0 &\mbox{otherwise}.\end{cases}$$ a) What is the first time $t_0$ where a shock forms?
b) Sketch solution at time $t=2$.
c) What is the shock velocity?
I'm a bit confused where to start, any help would be appreciated thanks!
Here is a basic methodology that you can apply and work out the details for specific initial data.
You can use the method of characteristics to find an implicit solution.
The characteristics are determined by the IVP
$$\frac{dX}{dt}= u(X(t),t),\\X(0) = x_0.$$
If $u$ is differentiable , we have
$$\frac{d}{dt}u[X(t),t]= u_t(X(t),t) + u_x(X(t),t)\frac{dX}{dt}=u_t(X(t),t) + u(X(t),t)u_x(X(t),t)=0.$$
Hence, along a characteristic curve $u(X(t),t)$ is constant
$$u(X(t),t)= u(X(0),0)=f(x_0).$$
Solving for $X(t)$ we obtain
$$X(t) = x_0 + f(x_0)t.$$
Therefore, $u(x,t)=f(x_0)$ at a specific point $(x,t) $with $t > 0$ -- where $x_0$ is the solution to $x_0 = x - f(x_0)t$.
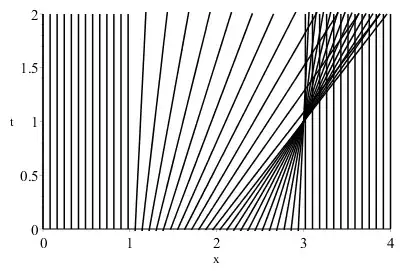
If two characteristics cross, then the solution becomes multi-valued. This can be interpreted as the formation of a discontinuity or shock. The first time this happens is determined is follows.
Consider two characteristics initiated at points $(y,0)$ and $(y + \delta,0)$, respectively. If they intersect at time $t$ then
$$y + f(y)t = y + \delta + f(y + \delta)t$$
and
$$t = \frac{\delta}{f(y)-f(y+\delta)}$$
The earliest possible time for the formation of a shock is then given by
$$t_s = \inf_{y} \lim_{\delta \rightarrow 0} \frac{\delta}{f(y)-f(y+\delta)}=\inf_{y}\frac{-1}{f'(y)}.$$
Suppose a shock is located at position $x_S(t)$ with $u(x,t) = u_L$ if $-\delta < x < x_S(t)$ and $u(x,t) = u_R$ if $\delta >x > x_S(t).$
Then,
$$\frac{d}{dt}\int_{-\delta}^{\delta} u(x,t) \, dx = \int_{-\delta}^{\delta} u_t \, dx = -\int_{-\delta}^{\delta} uu_x \, dx \\= -\int_{-\delta}^{\delta} \frac{\partial}{\partial x}\left(\frac1{2}u^2\right) \, dx = \frac1{2}(u_L^2-u_R^2).$$
Also,
$$\frac{d}{dt}\int_{-\delta}^{\delta} u(x,t) \, dx =\frac{d}{dt}\left[u_R(\delta-x_s)+u_L(x_s+\delta)\right]=\frac{dx_S}{dt}(u_L-u_R).$$
Hence,
$$\frac{dx_S}{dt}(u_L-u_R)=\frac1{2}(u_L^2-u_R^2),$$
and the shock propagates at a speed given by
$$\frac{dx_S}{dt} = \frac1{2}(u_L + u_R).$$
Let us complete the answer by @RRL.
a) The breaking time is $$t_b = \frac{-1}{\inf f'} = 1$$
b-c) This is illustrated on a sketch of the characteristic curves in the $x$-$t$ plane:
On both sides of the shock, the solution at $t>1$ is deduced from the method of characteristics $u = f(x-ut)$. Hence, $u$ is equal to $\frac{x-1}{1+t}$ or zero on each side of the shock. To compute, the shock trajectory $x_s(t)$ with the shock velocity $\dot x_s(t)$, we apply the Rankine-Hugoniot condition $$ \dot{x}_s(t) = \frac{1}{2} \left(\frac{x_s(t)-1}{1+t} + 0\right) ,\qquad x_s(1) = 3 , $$ which gives $x_s(t) = 1 + \sqrt{2 (1+t)}$ and $\dot x_s(t) = \sqrt{2(1+t)}^{-1}$. At $t> 1$, the solution is $$u(x,t) = \left\lbrace \begin{aligned} &0 &&\text{if}\quad x<1 \quad\text{or}\quad x > 1 + \sqrt{2 (1+t)} \\ &\frac{x-1}{1+t} &&\text{if}\quad 1\leq x < 1 + \sqrt{2 (1+t)} \end{aligned} \right. $$