1

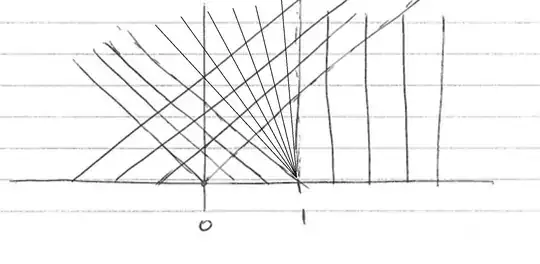
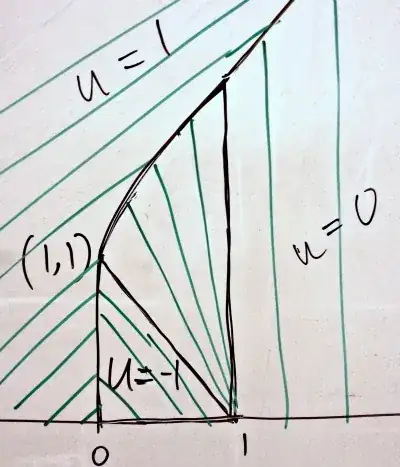
I'm looking for the equations of the characteristics of the fan of the Burgers equation $$\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}=0,\quad x\in\mathbb{R}, \ t>0$$ with initial condition $$ u(x,0) = \begin{cases} 1,\quad &x<0\\ -1,\quad &0<x<1\\ 0,\quad &x>1 \end{cases} $$

My solution

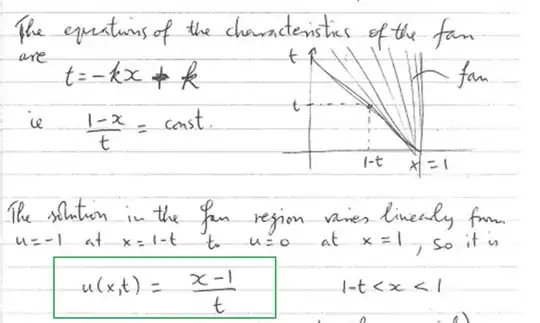
enter image description here

To find the equation in the green box would I be correct in saying that because $u$ is constant on the charachteristic curves $\frac{dx}{dt}=u$ i.e

$x=ut+1$ as $x(0)=1$, which implies

$u=\frac{x-1}{t}$?

enter image description here

usainlightning
  • 1,217
  • You would likely avoid downvotes by typing out at least the problem statement. –  Apr 05 '15 at 01:54

1 Answers1

0

Yes, within the fan (expansion/rarefaction) region $u(x,t)=(x-1)/t$. A simple geometric explanation is that all characteristics there emanate from $(1,0)$, which gives $(x-1)/t$ as their $\Delta x/\Delta t$ slope.

It's important to note that the boundary of the expansion region is complicated. Here is a sketch [with a typo: $(1,1)$ should be $(x=0,t=1)$.]

sketch

The curvilinear part of the boundary satisfies the ODE $$ \frac{dx_b}{dt} = \frac12\left(1+\frac{x_b-1}{t}\right),\qquad x_b(1)=0 $$ fromw where you can find its equation $x_b(t)$ (hint: it's quadratic polynomial).

  • Why do the charachteristic lines stop after they cross with a charachteristic emanating from another 'region'? i.e Why do the lines where $u=-1$ carry on beyond their initial cross with there where $u=1$? – usainlightning Apr 05 '15 at 10:38
  • If two characteristic lines crossed, the function $u$ would have two different values there (according to the slope of the lines). Read about shock waves here –  Apr 05 '15 at 15:24
  • I understand that however normally when we sketch charachterstic diagrams, we sketch the entire line so that each charachteristic line intersects many times, as in the graph I have added to the OP. So I am a bit confused. Don't the secondary, tertiary crossings etc. represent shocks also but at a later time? – usainlightning Apr 05 '15 at 16:35
  • I also do not think my solution for the equations for the charachteristics is correct, as if $u$ is constant on each charachteristic, then as all of these chaachteristics emanate from the same point $u$ will be constant throughout the region which is incorrect. – usainlightning Apr 05 '15 at 17:40
  • On your first, rough, sketch, characteristics line may intersect. But when that happens, you should then understand how the shock forms and propagates, add shock waves to the diagram, and terminate characteristics at the shock. Then you'll have a correct diagram without intersections. See this answer for an example of two-stage process. –  Apr 05 '15 at 17:54
  • For your second comment: your characteristics are correct. They emanate from a point of discontinuity, which is a special situation. The value of $u$ at a discontinuity point is not useful, it's better to ignore it at all. The value of u on each characteristic line is determined by the slope of that line. Again, I strongly recommend you to read up on solutions of Burgers' equation with discontinuous data (as in my link above). If you only dealt with continuous solutions up to now, you are going to make a lot of mistakes applying the same approach to discontinuities. –  Apr 05 '15 at 17:57