3

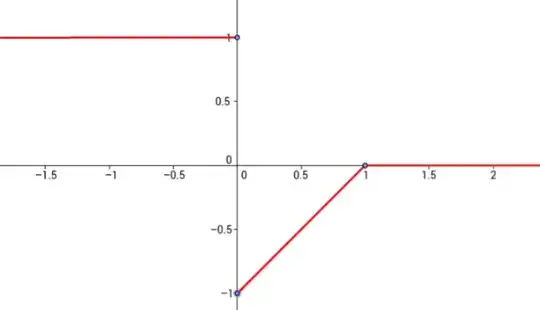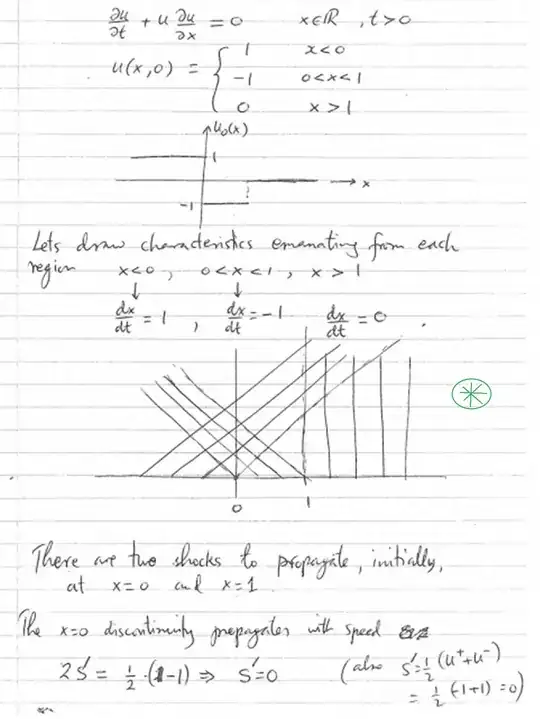
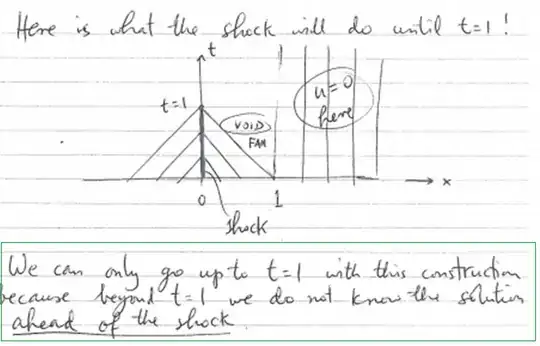
enter image description here enter image description here

I understand that we do not know the value of $u(x,t)$ when $0<x<1$ and $t≥1$ (because the charachtersitics do not pass through these points). However I am confused by 'ahead of the shock'.

If I sketch $u(x,t)$ at $t=1$ (with reference to the graph $\color{green}{(*)}$ as below by using the values of u after the shock at $x=0$ and before the shock have switched around.

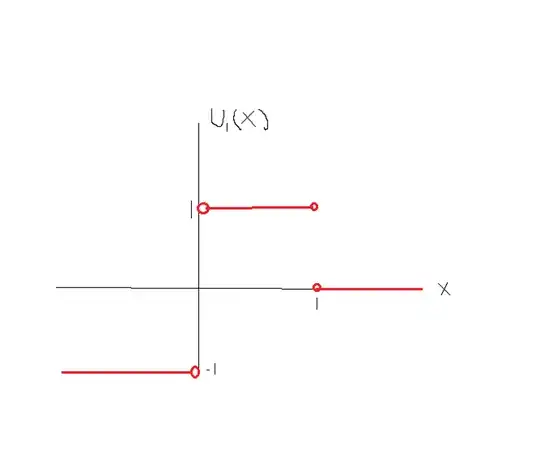
enter image description here

However my notes state that that up to $t=1$ the value of $u$ before the shock is $1$ and after it is $−1$. Where am I going wrong here?

  • I'm not sure exactly what is meant "we don't know"; the "void" is a rarefaction wave in which the solution can be found as here. By the way, this answer is about exactly the same problem. –  Apr 06 '15 at 01:14
  • Apologies I should have made it clearer that I was referring to the notes, I understand that it can be extended, so that there is a solution in the void. However, I would still like to check whether my graph of $u(x,1)=u_1(x)$ is correct and whether or not it contradicts the second of the charachteristic diagrams, where $u=1$ before the shock and $-1$ afterwards. –  Apr 06 '15 at 10:24
  • 1
    I wrote an explicit solution to a different initial condition here http://math.stackexchange.com/questions/1058321/entropy-solution-of-u-tu2-2-x-0 I hope it helps.once you get the hang of how to identify shocks, then it isn't all that bad. – DaveNine Apr 06 '15 at 18:52

1 Answers1

1

Your graph of $u(x,1)$ is not correct. Because characteristics do not go through each other; they terminate at the shock. My sketch here, with correctly trimmed characteristics, gives the true picture of $u(x,1)$:

plot

In a formula, $u(x,1)=1$ for $x<0$, $u(x,1)= x-1$ for $0<x<1$, and $u(x,1)=0$ for $x\ge 1$.

Community
  • 1
  • 1
    Many thanks, However I don't understand why it is that charachteristics terminate at the shock? –  Apr 06 '15 at 15:05
  • 1
    Shocks occur when characteristics intersect, which make finding a solution difficult. We're no longer able to use what we know about characteristics. – DaveNine Apr 06 '15 at 18:55
  • @lemony9201 This takes a while to explain. I recommend carefully reading everything on this page, omitting 3.5.3. Take-away point: "Physically, this [intersection of characteristics] is normally not acceptable: you can not have three different pressures or flow velocities at the same point." –  Apr 06 '15 at 18:59
  • 1
    @DaveNine I understand that shocks occur at the intersection of charachterisitics. However, a charachteristic may intersect with others many times as in $\color{green}{(*)}$. So are we not losing information about later shocks, by terminating the charachteristics? –  Apr 06 '15 at 19:55
  • 1
    We only care about the first intersection. The shock will imply that the direction of those characteristics will change. There's an analogy to waves to be made here, if two waves intersect eachother at the same speed then a different wave is created in a different direction(we find this direction by the rankine-hugonoit condition from the shock). So we aren't losing information, in fact we're gaining information by knowing when/where the shock occurs first. A solution then may be built from that information. – DaveNine Apr 06 '15 at 19:59
  • 1
    @DaveNine Why as in this example link do we not ignore the values of $u$ in the fan emanating from $(1,0)$ even though all of the charachteristics of the fan cross at $(1,0)$? –  Apr 07 '15 at 00:43