2

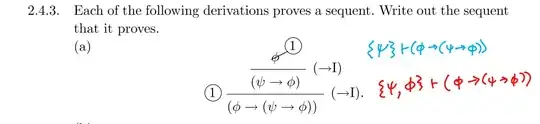
Trying to learn sequent calculus and so I am trying to work thru some examples to get a better grip/understanding but the following question is not answered at the back of the book. I wrote my guess in the blue writing in the attached picture, however I am unsure of my answer because phi appears in the consequent under the first line. So I am wondering if it should look like my second guess which is written in red. The book I took this from is Mathematical Logic, by Hodges. Hope somebody can explain what is correct and why, please!!!

enter image description here

skyfire
  • 815

2 Answers2

3

It is meant to prove the sequent $\vdash\phi\rightarrow (\psi\rightarrow\phi)$, but the derivation is not complete. The first $(\rightarrow I)$ needs the assumption $\psi$ (and repeating the assumption $\phi$):

From "Logic in computer science" (Huth & Ryan) page 20:

Logic in computer science, Huth & Ryan

Also note that your derivation is in Natural Deduction and it's different from Sequent Calculus (since you said you are trying to learn Sequent Calculus)

Community
  • 1
LoMaPh
  • 1,361
  • 1
    Mauro is correct, another way to view the suddenly appearing premise is thru the addition rule combined with viewing the implication as a disjuction (material implication). – skyfire Apr 25 '15 at 14:18
  • Albeit I initally agreed with you, which was why I was so confused by the book posing the question in that way. – skyfire Apr 25 '15 at 14:21
  • @skyfire - Brilliant ! We have : $\phi \vdash \phi \vdash \lnot \psi \lor \phi$ by $\lor$-introduction ... – Mauro ALLEGRANZA Apr 25 '15 at 15:00
  • 1
    @skyfire - but note that both rules $\to$-intro and $\lor$-intro are intuitionistically valid, while the equivalence between $p \to q$ and $\lnot p \lor q$ is not ... – Mauro ALLEGRANZA Apr 25 '15 at 15:11
  • We can always introduce new rules as shorthands for a combination of "basic" rules. The reason I said it is not complete was that if we want to use only the basic rules of natural deduction, then we need a longer derivation. For example, the derivation of $p\lor\neg p$ in Natural Deduction is not very short, but you may just derive it in one step and use it in derivations as a "new rule", because you know it is provable. But I believe in these cases it is better to use a symbol different from the basic rule names. For example use $Abr$ (abbreviation). @MauroALLEGRANZA – LoMaPh Apr 25 '15 at 20:01
2

Neither.

The sequent proved is :

$\vdash (\phi \to (\psi \to \phi))$.

It is the last formula and the only assumption of the derivation : $\phi$, has been discharged (it is crossed with the "dandah").

The derivation is correct; see the discussion in :

or see the relevant parts quoted into this post.

The approach followed by Chiswell & Hodeges into this example simply amounts to :

we can discharge any assumptions, also assumptions not "declared" as such in the derivation.

The intuition behind it is quite simple : let's start assuming $\phi$, and derive $\phi$.

Having preformed this obviuos derivation of $\phi$ from some assumptions, it is harmless to assert that we have derived it from "those" assumption plus some extra-one.

Conclusion : we can always add "unnecessary" assumptions in a derivation.

Community
  • 1
Mauro ALLEGRANZA
  • 94,169