7

I'm currently learning about parallel transport and connections and we were considering the parallel transport of a tangent vector along a sphere as given in the picture below.

enter image description here

From my understanding, by defining a connection on your manifold, you provide a way to identify vectors at one point of the manifold with vectors at another point on the manifold via parallel transporting the vector.

So in the given example, when the initial vector is parallely transported along the closed curve it returns to the same spot as a different vector. Is this because there has not been defined a correct connection on the sphere (that takes into account the curvature of the 2-sphere)? In which case, when a connection is defined on the sphere, (i.e. by the covariant derivative) parallel transport of any vector along a closed curve back to its initial position will result in the same vector?

So this is in fact an example of the need for a connection, and not just the standard derivative?

Thanks in advance!

Bobby
  • 105
  • What do you mean by «the standard derivative»? – Mariano Suárez-Álvarez Aug 18 '15 at 07:57
  • By the way, it is not true that parallel transport along a closed curve on the sphere maps a vector to itself. – Mariano Suárez-Álvarez Aug 18 '15 at 07:59
  • Now that it is a question instead of a claim: never. No matter what the metric on a sphere is, there are always points where the curvature is positive (this follows from the Gauss-Bonnet theorem, for example) so there are small closed curves along which parallel transport is not the identity. – Mariano Suárez-Álvarez Aug 18 '15 at 08:04
  • I mean the covariant derivative can be defined $\nabla_u v=D_u v+ \Gamma {u,v}$ (I got this equation off wiki), I thought maybe the reason the vector changed after being parallel transported was because the second term of the equation $\Gamma$ was being neglected.

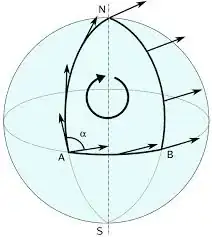
    If this is not the case, and any vector, when parallel transported on a closed curve returns to the same position as a different vector, how can the connection provide a well-defined way to transfer vectors along the 2-sphere?

     – Bobby Aug 18 '15 at 08:09
  • I suggest you try a textbook on the subject and not wikipedia. WIkipedia is often not a good place to learn things such as this. – Mariano Suárez-Álvarez Aug 18 '15 at 08:16
  • Apologies, I only stated the wiki reference incase you wanted to investigate how it was defined. None-the less this same equation was derived for us in my lecture which is why I didnt fear including it, despite it coming from wiki. – Bobby Aug 18 '15 at 08:21

2 Answers2

4

From my understanding, by defining a connection on your manifold, you provide a way to identify vectors at one point of the manifold with vectors at another point on the manifold via parallel transporting the vector.

Parallel transport depends on 1. a Riemannian manifold $(M, g)$, for example the round unit sphere; 2. a pair of points $p$ and $q$ of $M$, not necessarily distinct; 3. a piecewise-smooth path $\gamma:[0, 1] \to M$ starting at $p$ and ending at $q$, i.e., satisfying $p = \gamma(0)$ and $q = \gamma(1)$. (It's not essential that the parameter interval be the unit interval $[0, 1]$; an arbitrary closed, bounded interval will do.)

A Riemannian metric induces a Levi-Civita connection. In your example, the round sphere has a connection already, for which a tangent vector to a great circle arc remains tangent to the arc under parallel transport along the arc.

The example of the round sphere demonstrates dependence of parallel transport on $\gamma$. If $\gamma$ were a constant path, or a great circle arc traced forward and backward, parallel transport along $\gamma$ would be the identity map. For the spherical triangle $\gamma$ in your diagram, parallel transport along $\gamma$ is not the identity.

To emphasize (what seems to be) the underlying issue: The path $\gamma$ is a crucial piece of data in parallel transport; there's no well-defined notion of "parallel transport from $p$ to $q$" except in very special circumstances, such as parallel transport in a Euclidean plane, or on a flat torus. (Flatness—identically-vanishing Gaussian/sectional curvature—is necessary but not sufficient.)

Andrew D. Hwang
  • 78,195
  • Yes, this is exactly the part im not getting! So in order for a connection to provide a way to identify vectors at one point of the manifold to vectors at a different point, the path parallelly transported along would need to be specified? – Bobby Aug 18 '15 at 09:44
  • Yes. :) Analytically, parallel transport along a regular path $\gamma$ may be expressed in local coordinates as a linear system of ODEs, i.e., as an ODE for a vector-valued function. A tangent vector $v_{0}$ at $p$ provides an initial value for the ODE, and the value of the (unique) solution at time $1$, a tangent vector at $q$, is the result of parallel transporting $v_{0}$ along $\gamma$. – Andrew D. Hwang Aug 18 '15 at 12:56
2

I think you're confusing two distinct concepts. Here's an informal but hopefully intuitive explanation.

The connection accounts for the fact that the coordinate basis vectors in a curvilinear coordinate system change with the coordinates - e.g., in spherical coordinates, $\hat{\mathbf{e}}_r$, $\hat{\mathbf{e}}_\theta$, $\hat{\mathbf{e}}_\phi$ depend on $(\theta,\phi)$.

The regular derivatives $\partial/\partial\xi^i$ aren't sufficient to correctly express the change in a field between neighbouring points because the field values and the coordinate basis vectors change from $\xi^i$ to $\xi^i + d\xi^i$. The covariant derivative includes the connection coefficients to account for that extra change. Note that the connection coefficients are coordinate-system dependent.

On the other hand, the fact that parallel-transporting the tangent vector around a closed curve in a given manifold doesn't always give you the tangent vector you started with is an indication of the local curvature of the manifold in question, and is independent of the coordinate system chosen to cover the manifold with because local curvature is an intrinsic property of the manifold. In fact, looking at the parallel-transport of the tangent vector around a closed curve is one way to define the Riemman tensor.

wltrup
  • 3,983