I need to transport a tangent vector on 2-sphere from point $p$ to $q$ along the geodesic, which is defined using great circles in this case. I believe there are iterative solutions to achieve that like explained here. Is there a close form solution to achieve that?
Asked
Active
Viewed 1,267 times
2 Answers
4
Yes, you want to apply the unique rotation matrix that sends $p$ to $q$ while preserving their cross product. Computing that rotation matrix is a well-known problem, e.g.:
Calculate Rotation Matrix to align Vector A to Vector B in 3d?
Stack Overflow: Finding quaternion representing the rotation from one vector to another
Chris Culter
- 26,806
3
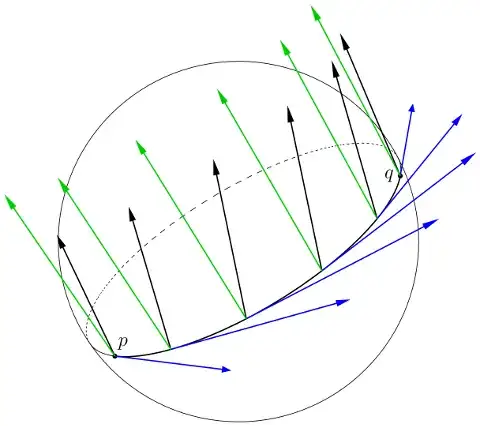
$\require{begingroup}\begingroup\newcommand{\Reals}{\mathbf{R}}\newcommand{\Basis}{\mathbf{e}}$Explicitly, assume $p$ and $q$ are distinct, non-antipodal unit vectors (points on the unit sphere in $\Reals^{3}$). Introduce the orthonormal basis $$ \Basis_{1} = p,\qquad \Basis_{3} = \frac{p \times q}{\|p \times q\|},\qquad \Basis_{2} = \Basis_{3} \times \Basis_{1}, $$ and let $c = p \cdot q$, so that $$ q = c \Basis_{1} + \sqrt{1 - c^{2}} \Basis_{2}. $$
Under parallel transport along the great circle arc $$ \gamma(t) = (\cos t) \Basis_{1} + (\sin t) \Basis_{2}, \tag{1} $$ $\Basis_{2}$ (blue) is carried to $(\cos t) \Basis_{2} - (\sin t) \Basis_{1}$, while $\Basis_{3}$ (green) is preserved. Every tangent vector $v$ at $p$ (black) can be written as a linear combination $$ v = a \Basis_{2} + b \Basis_{3}, $$ and the parallel transport of $v$ along (1) from $p$ to $\gamma(t)$ is $$ \Gamma_{t}(v) = a(\cos t) \Basis_{2} - a(\sin t) \Basis_{1} + b \Basis_{3}. $$ $\endgroup$
Andrew D. Hwang
- 78,195