In "Random Construction of Riemann Surfaces", Robert Brooks and Eran Makover say :
Definition 2.1 A left-hand turn path on $(\Gamma, \mathcal O)$ is a closed path on [the cubic graph] $\Gamma$ such that, at each vertex, the path turns left in the orientation $\mathcal O$.
The genus of $S^O(\Gamma,\mathcal O)$ is given by $$ \text{genus}=1+\frac{n-l}2 $$ [$l$ is the number of left-hand paths.]
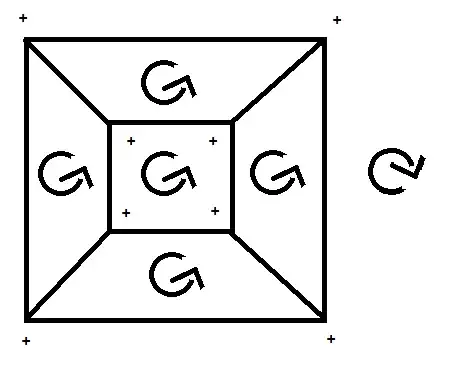
Note that the usual orientation on the $3$-regular graph which is the $1$- skeleton of the cube contains six left-hand-turn paths, giving that the associated surface is a sphere with six punctures, while a choice of a different orientation on this graph can have either two, four, or six left-hand-turn paths, so that the associated surface can have genus $0$, $1$, or $2$. Thus, the topology of $S^O(\Gamma,\mathcal O)$ is heavily dependent on the choice of $\mathcal O$.
There are $2^{8}$ orientation. What is the usual one? How do these paths look like. An illustrative example is sought, because my brain starts to feel like a punctured sphere...
EDIT:
Does the usual orientation mean that we just assign a "$+$"-orientation, which should mean that we look at it like it is displayed? A "$-$" would flip the meaning of left and right. In this case the following would give the right number of left-hand cycle: