1

When you draw a planar cubic bipartite graph $\Gamma$ and 3-color its edges you can use this as an orientation $\mathcal O$.

Definition A left-hand turn path on $(\Gamma, \mathcal O)$ is a closed path on $\Gamma$ such that, at each vertex, the path turns left in the orientation $\mathcal O$.

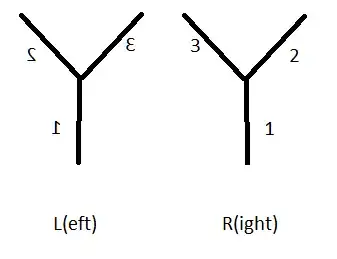
I want to calculate the number of left-hand turn paths of $\Gamma$ without drawing them. I found the following: When you look at a vertex with the given (planar) edge-coloring i.e. orientation, there are two situations that can happen:

$\hskip1.7in$enter image description here

Lets start with the left figure: When you come from the color-1 edge and you want to go left you end at the color-2 edge. Coming from 2 you end at 3, and from 3 to 1.

Fine in the right figure the orientation is inverted, so left is right here. So if we come from the color-1 edge we end at (surprise,surprise) the color-2 edge. And so forth...

So after 1 follows 2 after that 3 and then 1 again, no matter if we reach a left- or right-oriented vertex.

Now, the adajency matrix of the graph $A_\Gamma$ splits up into three different color submatrices, with $A_\Gamma=A_1+A_2+A_3$. $A_k$ are permutation matrices with $A_k^2=1$.

So the number of left-hand turn path can be calculated when you look at the number of unique solutions of $$(A_3A_2A_1) v_kv_{k+1} =v_kv_{k+1},$$ where $v_k$ can be any vertex as starting point and $v_kv_{k+1}$ indicates the starting edge. Vertices are allowed multiple times. Edges may be traversed in the opposite directions as well...

Is this correct and if so are there other ways to do it?

draks ...
  • 18,449
  • Isnt your claim equivalent to "an orientation on a cubic graph is the same as edge 3-colouring"? Some cubic graphs do not admit edge 3-colourings. – SashaKolpakov Feb 05 '16 at 13:11
  • @SashaKolpakov I restrict to planar cubic ones where a 3-edge coloring is guaranteed by the 4-color theorem. An orientation can be chosen without respect to the edge coloring, e.g. All orientations can be left (or + as in my other post... – draks ... Feb 05 '16 at 14:46
  • 1
    some colouring is guaranteed, yes would you like the number of left turn paths with the orientation induced by that colouring? I'm worried by the fact that orientation means colouring half-edges around each vertex, and thus an orientation will produce an edge colouring only when all half-edge colours agree on the halfs of all edges. – SashaKolpakov Feb 06 '16 at 15:36
  • @SashaKolpakov yes, how many path for a given coloring / orientation. Is my proposed way correct? I think your worries are no problem for planar graphs... – draks ... Feb 06 '16 at 15:51
  • 1
    Do you want to count cycles (closed loops) or paths (which can start and end anywhere)? If paths, do you allow a vertex to be used more than once? Or an edge? – Matt Feb 14 '16 at 22:30
  • @Matt Cycles. Vertices are allowed multiple times. Edges may be traversed in the opposite directions as well... – draks ... Feb 15 '16 at 06:19
  • So, to summarize, each edge can be used at most once in each direction, and so a vertex can be used up to three times. When your next step would take the same edge (in the same direction) as your first step, you have closed the cycle. – Matt Feb 15 '16 at 15:28

1 Answers1

1

Solving your equation $(A_1A_2A_3)^t v_kv_{k+1} =v_kv_{k+1}$ will count each cycle multiple times, even if you only consider the minimal positive $t$ that works, since each cycle will be counted once for every $3\rightarrow 1$ transition it contains (and it must contain an even number of them, since the graph is bipartite).

Since the $A_k$ are permutation matrices, the matrix $M=A_1A_2A_3$ is itself a permutation matrix, and what you want is exactly the number of cycles in this permutation $\pi_M$. Since the graph is bipartite, every cycle of $\pi_M$ will be of even length, corresponding to a unique "left hand turn" cycle in $\Gamma$ that is three times longer. Clearly each cycle in $\pi_M$ corresponds to a unique "left hand turn" cycle in the graph, and vice versa.

You might be worried that $\pi_M$ could have cycles where we return to a vertex but we are traveling in the opposite direction and so it is not really a cycle. But this cannot happen, since every vertex in a cycle of $\pi_M$ is always being traversed in the $3\rightarrow 1$ direction. If we return to a vertex, we are passing through it in exactly the same way.

Matt
  • 9,223
  • Thanks, do you think it is possible to calculate the number cycles with some properties of $M$ like eigenvalues...? – draks ... Feb 15 '16 at 15:38
  • Different cycles of the same length will yield the same eigenvalues, see this answer. Finding the cycles directly (and counting them) is faster and simpler than computing eigenvalues anyway. The number of cycles is a property of $M$. What are you looking for: something easy to implement in a particular programming language, or perhaps a formula with a certain mathematical form? – Matt Feb 15 '16 at 16:56
  • Also see this answer. – Matt Feb 15 '16 at 17:26
  • Thanks, for the links. A formula with a certain mathematical form sounds appealing. I agree that cycles are counted multiple times To me it feels like I could go through all pairs $v_kv_{k+1}$, .i.e. edges $e_j$ cycle through them and count. Do you think this would be easier if I use the line graph of $\Gamma$? – draks ... Feb 16 '16 at 06:38
  • If you replace each edge with two oppositely directed edges, and split each vertex into three vertices (for the three ways the path could go through that vertex), then the resulting graph is exactly the cycles you are looking for. The line graph is similar, but it doesn't distinguish between the two directions of each edge, making it hard to use. – Matt Feb 16 '16 at 22:24
  • Could you a drawing? I don't get what is connected to what after splitting each vertex into three... – draks ... Feb 17 '16 at 06:47
  • Every edge splits into two edges, one oriented in each direction. So the edge $AB$ splits into $A\rightarrow B$ and $B\rightarrow A$. This makes every vertex degree-6. Now each degree-6 vertex splits into three disjoint parts. One part is the incoming 1 edge connected (with a degree-2 vertex) to the outgoing 2 edge. The other 2 parts are similar. I can't put a picture in the comment, but kind of like this. – Matt Feb 22 '16 at 00:15
  • Okay, let's say $B$ is also connected to $C$ and $D$. How do you make up your degree-2 vertex: ingoing from $A$ and outgoing to $C$ or $D$, depending on which is left from $A$? (BTW: Usually I upload pictures in a post to get the stack.imgur reference and then cancel the edit...) – draks ... Feb 22 '16 at 06:26
  • Yes, exactly like that. – Matt Feb 22 '16 at 08:18