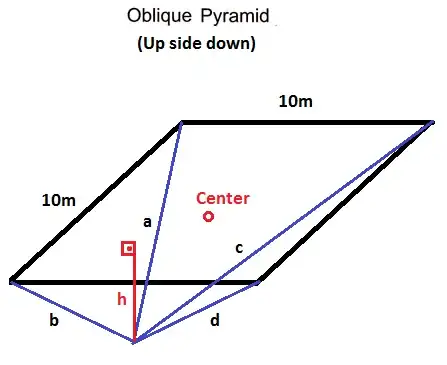
I have a kind of Oblique Pyramid. I use this structure up side down. Tip of the pyramid is looking towards down. All four legs of the pyramid are wire lines and connected to winding motors on the corners of the base. Base is square 10m x 10m. I am able to move the tip of the pyramid within the perimeter using motors. Some are winding some are unwinding while I am doing this.
So, I know exact lengths of the 4 lines ($a$, $b$, $c$, $d$) and the perimeter sizes (10m x 10m x 10m x 10m). Can I calculate the height of the tip of the pyramid with those variables? If yes, what would be the equation(s)?