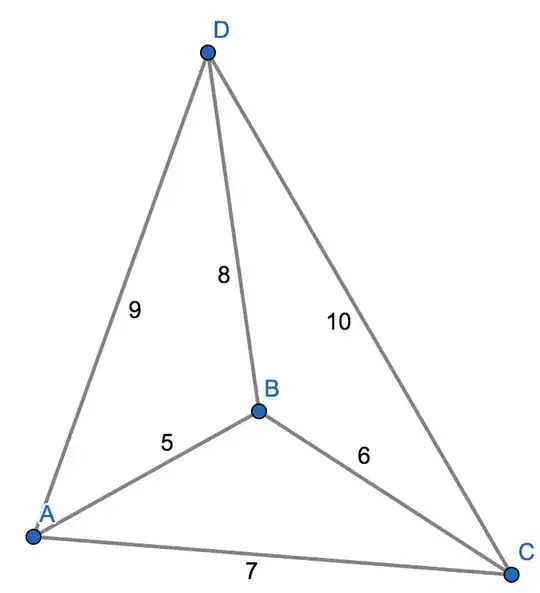
We know that the volume of a tetrahedron is one-third the area of the base times the height, so if we can find the are of $\triangle ABC$ and the volume of the tetrahedron, we are home free. We can find the area of a triangle, given the lengths of the sides, by Heron's formula. At the bottom of the same Wikipedia page, there is a Heron-type formula for the volume of a tetrahedron, due to David Robbins. It doesn't look pleasant, but it should do the job.
I found another discussion of a tetrahedral volume formula (due to the renaissance painter Pierro della Francesca!) in Kevin Brown's Math Pages. Some care is necessary in using the formula, because as explained in the article, the formula depends on the pairings of opposite sides of the tetrahedron, and there are actually two tetrahedra, with different volumes, for a given pairing of six lengths. This is a complicated formula also, but it doesn't have all those square roots!
EDIT
Alternatively, just solve it with coordinate geometry. Here's a python script
from sympy.core.symbol import symbols
from sympy.solvers.solveset import nonlinsolve
# A(0,0,0)
# B(u,v,0)
# C(0,7,0)
# D(x,y,z)
# AB = 5
# AC = 7
# BC = 6
# AD = 9
# BD = 8
# CD = 10
u,v,x,y,z = symbols('u,v,x,y,z', real=True)
equations = (u**2+v**2-25,
u**2+(7-v)**2-36,
x**2+y**2+z**2-81,
x**2+(y-7)**2+z**2-100,
(x-u)**2+(v-y)**2+z**2-64)
solns = nonlinsolve(equations, [u,v,x,y,z])
for soln in solns:
print(soln)
This produces the output
(-12*sqrt(6)/7, 19/7, -31*sqrt(6)/21, 15/7, -sqrt(570)/3)
(-12*sqrt(6)/7, 19/7, -31*sqrt(6)/21, 15/7, sqrt(570)/3)
(12*sqrt(6)/7, 19/7, 31*sqrt(6)/21, 15/7, -sqrt(570)/3)
(12*sqrt(6)/7, 19/7, 31*sqrt(6)/21, 15/7, sqrt(570)/3)
so that the height is $\boxed{{\sqrt{570}\over3}}\approx7.95822425754$
You should check that the solutions actually satisfy the given conditions, because I haven't done that.