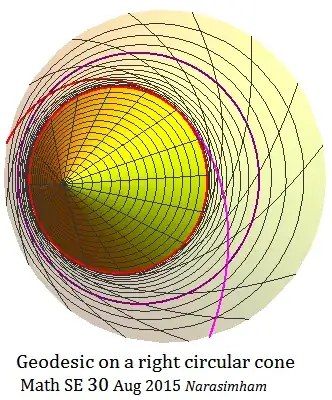
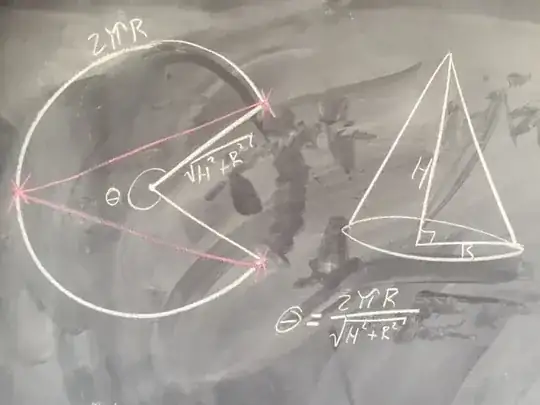
An exact way is .... if radius at closest point to axis of symmetry near cone vertex is $r_{min}$ and cone semi-vertical angle
$$ \alpha = \sin ^{-1} \frac{R}{\sqrt { R^2+H^2}}, $$
then
$$ r_{min} = r \cos ( \theta\cdot \sin \alpha) $$
Arc lengths and geodesics are obtained by integration using :
$$ ds^2 = dr^2 + dz^2 + ( r d \theta)^2 $$ and using Clairaut's Law:
$$ r_{min}= r^2 \cdot \frac{d \theta }{ ds } = r \cdot \sin \psi $$
EDIT 1:
which gives
$$\frac{d \psi}{ds} = - \sin \alpha = -\frac12, $$
say as an example of $30^0$ semi-vertical angle cone. Then we must have
$$ \psi= (\pi/4, \pi/2, 3 \pi/4 ) $$
respectively at points of (entry, $r_{min}$, exit) of geodesic line on the truncated cone. If R = 1, these radii are accordingly $( 1, 1/\sqrt 2, 1 ). $
Calculation of radius and arc length of cone /geodesic from middle position:
$$ dr / \sin \alpha = r d \theta \cot \psi$$
$$ dr / \sin \alpha = r d \theta \sqrt{(r/r_{min} )^2-1 }$$
Integrating , integration constant =0 with central boundary condition
$$ r = r_{min} \sec ( \theta \sin \alpha ); z = r \cot \alpha = r_{min}\cdot \cot\alpha\, \sec ( \theta \sin \alpha ) \tag {1} $$
which is the required equation of polar projection of geodesic.
Considering differential lengths/angles
$$ d \theta /ds = \sin \psi /r = r _{min} /r^2 $$
plug in from above and integrate
$$ s/r_{min} = \tan (\theta \, \sin \alpha ) / \sin \, \alpha \tag{2} $$
which is general equation of (semi) arc length of geodesic arc.
For $ \alpha =0 $, or $ \pi/2 $ we have $ s = r _{min} \tan \theta $ as we can expect.
Again plugin from (1) for semi-arc lengthFor
$$ s /r = \sin ( \theta \sin \alpha )/\sin \alpha $$
At the requiredparticular diametrical opposite position $ \theta = \pi/2 $ the full arclength $$ = \sqrt{R^2+H^2}\sin ( \pi R/(2 \sqrt{R^2+H^2})) \tag {3} $$
However it is more convenient to retain $(r-\theta, s- \theta)$ forms.