Given 4 integers, $a, b, c, d > 0$, does $\frac{a}{b} < \frac{c}{d}$ imply $\frac{a}{b} < \frac{a+c}{b+d} < \frac{c}{d}$?

Question

We were trying to come up with an easy way to generate a rational number in between two existing rational numbers with a fairly low numerator and denominator (the way we were doing this earlier was to find the average of the two rationals, but that results in a denominator of up to $c * d$. Does this inequality hold for all values of $a, b, c, d$?

Answer 1

Yes, the inequality holds. One standard approach to proving that $x\lt y\,$ is to show that $y-x\gt 0$.

Apply this to $x=\dfrac{a}{b}$ and $y=\dfrac{a+c}{b+d}$.

The difference is $\dfrac{a+c}{b+d}-\dfrac{a}{b}$, which simplifies to $\dfrac{bc-ad}{(b+d)b}$. But $bc\gt ad$ follows from our initial inequality.

The same method works for showing that $\dfrac{a+c}{b+d}\lt \dfrac{c}{d}$.

Answer 2

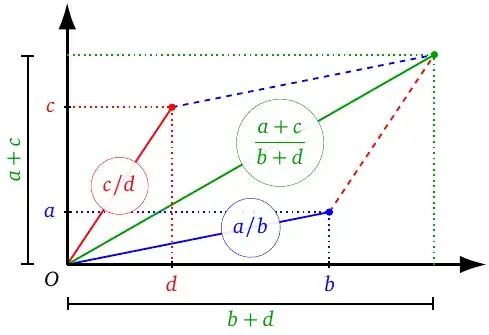
Hint $\ $ The middle term $\large \color{#0a0}{\frac{a+c}{b+d}}\:\!$ (known as the mediant), is the slope of the diagonal of the parallelogram with sides being the vectors $\color{blue}{(b,a)},\ \color{#c00}{(d,c)}.\:$ Clearly the slope of the diagonal lies between the slopes of the sides.

$\quad$

Answer 3

That follows from the slightly more general statement:

For $a_1, \ldots, a_n \in \Bbb R$, $b_1, \ldots, b_n > 0$ we have $$ \min_i \frac{a_i}{b_i} \le \frac{a_1 + \ldots + a_n}{b_1 + \ldots + b_n} \le \max_i \frac{a_i}{b_i} \, , $$ and equality holds if and only if $\frac{a_1}{b_1} = \frac{a_2}{b_2} = \dots \frac{a_n}{b_n}$.

(Note that the numerators need not be positive.)

Proof: Define $$ L =\min_i \frac{a_i}{b_i} \quad, \quad U = \max_i \frac{a_i}{b_i} \, , $$ then $$ \tag{*} b_i L \le \underbrace{b_i \frac{a_i}{b_i}}_{a_i} \le b_i U \quad \text{for $i=1, \ldots, n$} $$ and adding these inequality gives $$ L (b_1 + \ldots + b_n) \le a_1 + \ldots + a_n \le U (b_1 + \ldots + b_n) \, . $$ Equality holds if and only if equality holds in $(*)$ for all $i$, i.e. if all quotients $a_i/b_i$ are equal.

Answer 4

This is called the mediant. The inequality does indeed hold for all $a,\ b,\ c,\ d$.

Answer 5

Weighted average of two numbers with positive weight lies between the two numbers.

$$ x<y\phantom{x}\leftrightarrow\phantom{x}x<\frac{b}{b+d}\cdot x+\frac{d}{b+d}\cdot y<y $$

Now substitute $x=\frac{a}{b}$ and $y=\frac{c}{d}$

Answer 6

The setting where this occurs as a matter of course is simple continued fractions for, in this case, some positive quantity. If the "partial quotient" is some $k$ that is not necessarily equal to $1,$ the two related cases of the next "convergent" are $$\frac{a}{b} < \frac{a+kc}{b+kd} < \frac{c}{d},$$ which is what you get if the two convergents happen to be in increasing order, otherwise $$ \frac{c}{d} > \frac{c + ka}{d + kb} > \frac{a}{b}$$ where the inequality signs need to be massaged as the two convergents happen to be in decreasing order. Anyway, both displayed inequalities are true.

See SIMPLE