8

I was watching a numberphile video, and it stated that the limit of $1-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\cdots$ was $\frac \pi 4.$

I was just wondering if anybody could prove this using some terms and math I am likely to understand. I am a high school student taking Algebra II.

Travis
  • 3,396
  • 6
  • 23
  • 44
  • 3
    I am afraid that you need calculus to understand the proof. –  Jan 10 '17 at 20:47
  • I think there are some elementary ways of deriving the arctangent series. – Michael Hardy Jan 10 '17 at 20:48
  • @YvesDaoust : There are particular proofs that cannot be understood without calculus. Can you prove the non-existence of a different proof for which knowledge of derivatives (etc.) is not needed? – Michael Hardy Jan 10 '17 at 20:49
  • @MichaelHardy: I didn't claim that. Anyway, $\pi$ being a transcendental number, the recourse to infinity seems unavoidable. The historical discovery was based on integral calculus. –  Jan 10 '17 at 20:55
  • 1
    Related: http://math.stackexchange.com/questions/849348/geometric-intuition-for-pi-4-1-1-3-1-5-cdots – Simply Beautiful Art Jan 10 '17 at 20:55
  • 1
    This is also related: http://math.stackexchange.com/questions/14815/why-does-this-converge-to-pi-4 – Simply Beautiful Art Jan 10 '17 at 20:56
  • @Watson I imagine that choice of link will be the best we'll get. – Simply Beautiful Art Jan 10 '17 at 21:00
  • It surprises me that you would even be able to comprehend an infinite series to the level needed to understand this sum, so good luck and I do hope you become awesome at math. – Simply Beautiful Art Jan 10 '17 at 21:08
  • If I may incline you, the geometric series is far simpler... and then you should learn calculus ( calculus is honestly not too bad ) and combine the two, you can derive things like this (with some effort). – Simply Beautiful Art Jan 10 '17 at 21:11
  • @Travis: without trigonometry it is even more challenging to explain you :( But what do you know about $\pi$, then ? –  Jan 10 '17 at 21:12
  • @YvesDaoust, it's the ratio of a circles circumference to it's diameter ie: $C = \pi\times d$ $\pi \approx 3.14159653589\ldots$ It's an irrational number, it can't be represented as $\frac{p}{q}$ – Travis Jan 10 '17 at 21:17
  • By the way, if you ever want to chat with me personally on things that may seem less answerable, like this question, or if you want to learn some calculus, I don't mind chatting with you. I use Discord btw. – Simply Beautiful Art Jan 10 '17 at 22:20
  • Thanks, @SimpleArt, I'm not sure if I ever will, but I'll keep that in mind. – Travis Jan 10 '17 at 22:22
  • :-P It's also on my profile page if you ever forget how to find me. And I'm on the "users" tab. :-) Ranking pretty high this year. – Simply Beautiful Art Jan 10 '17 at 22:28
  • This is simply the Dirichlet $\beta$ function evaluated at $n=1.~$ In general, all values of this function at odd values of its argument yield rational multiples of powers of $\pi,$ i.e., $\dfrac{\beta(2k+1)}{\pi^{2k+1}}\in\mathbb Q.~$ Related concepts are the Dirichlet $\eta$ function, for which $\dfrac{\eta(2k)}{\pi^{2k}}\in\mathbb Q,~$ and the Riemann $\zeta$ function, for which $\dfrac{\zeta(2k)}{\pi^{2k}}\in\mathbb Q.$ – Lucian Jan 10 '17 at 22:46
  • You're using the term "limit" incorrectly. The title of your question should be: Why is $1-1/3+1/5-1/7+\cdots = \pi/4?$ Either that or "Why is $\lim_{n\to \infty}\sum_{k=0}^{n}(-1)^{k}1/(2k+1) = \pi/4?$ – zhw. Jan 11 '17 at 00:41
  • @YvesDaoust : You said you NEED calculus. And that historically it came from integral calculus. Can you be specific about the historical claim? – Michael Hardy Jan 11 '17 at 18:08
  • @MichaelHardy: no harassment please. –  Jan 11 '17 at 21:19

2 Answers2

12

I am doing my best to only use simple notions, but the explanation will look very strange and indirect. We will start with geometry.

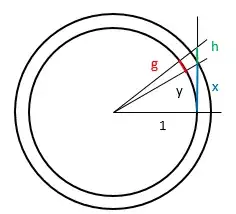
enter image description here

On the figure you see two right triangles, of basis $1$ and height $x$ and $x+h$ respectively. Note that $x$ and $h$ are line segments, while $y$ and $g$ arc circular arcs. We are particularly interested in the relation between the values of $y$ and $x$, which we will study by observing how the height difference $h$ makes the corresponding arc length $g$ vary.

By Pythagoras, the hypothenuses of the small triangle is $\sqrt{1+x^2}$, which is also the radius of the large circle. Then the arc facing $g$ on the larger circle has a length of $g\sqrt{1+x^2}$; if you straighten it, it becomes the base of the small outer triangle, which by proportionality has the length $(g\sqrt{1+x^2})\sqrt{1+x^2}$.

So we have established

$$\frac{g}{h}\approx\frac1{1+x^2}.$$

This relation is quite approximate in the figure, but if you make $h$ smaller and smaller, it becomes more and more accurate, because the arcs become more and more straight.

Actually, we just computed a derivative, i.e. the ratio of a variation of $y$ (from $y$ to $y+g$) over a variation of $x$ (from $x$ to $x+h$). This is a notion from calculus.

Now we want to express the relation between $x$ and $y$ and we will assume that it is of the polynomial type:

$$y(x)=a+bx+cx^2+dx^3+ex^4\cdots$$ without specifying the final degree. Using this formula, let us evaluate the ratio $g/h$, i.e.

$$\frac gh=\frac{y(x+h)-y(x)}h=\frac{a-a+b(x+h-x)+c((x+h)^2-x^2)+d((x+h)^3-x^3)+\cdots}h$$

For example, the cubic term gives, using a remarkable product

$$\frac{(x+h)^3-x^3}h=\frac{(x+h-x)((x+h)^2+(x+h)x+x^2)}h=(x+h)^2+(x+h)x+x^2.$$

If we again decrease $h$ so that it becomes neglectible compared to $x$, we obtain $3x^3$. Repeating this reasoning with all terms, you can check that we will get the polynomial expression

$$\frac gh=b+2cx+3\,dx^2+4\,dx^3+5\,dx^4+\cdots$$

We would like to compare it to the previous expression, which unfortunately is not in a polynomial form. We can achieve this goal by using the "geometric progression" formula.

Let us consider the numbers $(-x^2)^k$ and compute their sum for $k$ from $0$ to $n$:

$$S_n=1-x^2+x^4-\cdots(-x^2)^n.$$

Then if we multiply the sum by $-x^2$ and subtract, we obtain after a lot of terms cancellation

$$(1+x^2)S_n=1-(-x^2)^{n+1},$$ so that

$$S_n=1-x^2+x^4-\cdots(-x^2)^n=\frac{1-(-x^2)^{n+1}}{1+x^2}.$$

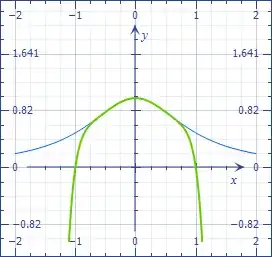
If $x^2<1$, then $(x^2)^n$ becomes smaller and smaller so that we can simplify

$$S_n=1-x^2+x^4-\cdots(-x^2)^n\approx\frac1{1+x^2},$$ and the larger the final degree, the better the approximation. The figure shows the matching of the polynomial of degree $10$ with the exact formula.

enter image description here

Now we are able to compare the formulas for $g/h$, and by identification,

$$b=1,c=0,d=-\frac13,e=0,f=\frac15,\cdots$$

Then, noting that $y(0)=0$, we also have $a=0$ and we establish the famous Gregory series, $$y(x)=x-\frac{x^3}3+\frac{x^5}5-\frac{x^7}7+\cdots$$ which is illustrated in the next picture (to degree $11$). It develops the so-called arc tangent function:

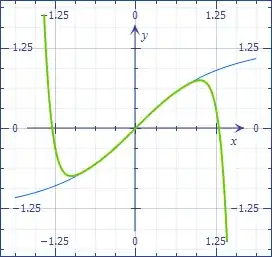
enter image description here

Finally, we can observe that when $x=1$, the arc $y$ covers an eighth of the circumference, hence the Leibnitz formula

$$\frac\pi4=1-\frac13+\frac15-\frac17+\cdots$$

The attentive reader may have noticed a little twist in the explanation. While obtaining the formula for $1/(1+x^2)$, we assumed that $x^2<1$, but later used $x=1$. For reasons that deserve many more explanations, the "polynomial" expression for $y(x)$ is still valid for $x=1$.

Michael Hardy
  • 1
3

If you have covered $$\arctan x=x-\dfrac{x^3}{3}+\dfrac{x^5}{5}-\dfrac{x^7}{7}+\cdots+(-1)^{n-1}\dfrac{x^{2n-1}}{2n-1}+\cdots\quad |x|\le 1$$ then, for $x=1$ $$\frac{\pi}{4}=\arctan 1=1-\dfrac{1}{3}+\dfrac{1}{5}-\dfrac{1}{7}+\cdots+(-1)^{n-1}\dfrac{1}{2n-1}+\cdots$$ $$$$

Fernando Revilla
  • 3,537