0

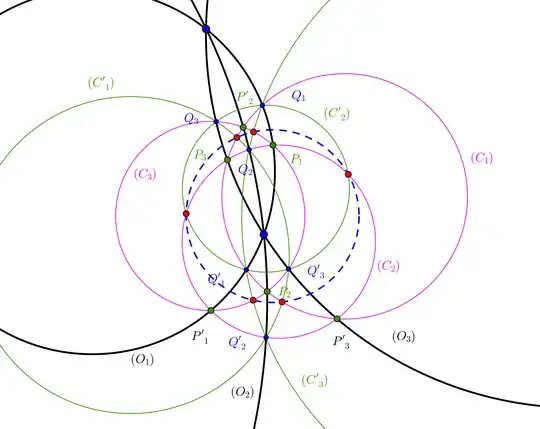
Continuing six points lie on a circle. I am looking for a proof of a problem as follows:

Let three circles $(O_1), (O_2), (O_3)$ are coaxial Circles. Let $P_1, P'_1$ lie on $(O_1)$, $P_2, P'_2$ lie on
$(O_2)$, $P_3, P'_3$ lie on $(O_3)$. Such that $P_1, P'_1, P_2, P'_2$ lie on a circle $(C_3)$, $P_2, P'_2, P_3, P'_3$ lie on a circle $(C_1)$ $P_3, P'_3, P_1, P'_1$ lie on a circle $(C_2)$. Let $(C_1) \cap (O_1) = Q_1, Q'_1$, $(C_2) \cap (O_2) = Q_2, Q'_2$, $(C_3) \cap (O_3) = Q_3, Q'_3$

Then show that: $Q_1, Q'_1, Q_2, Q'_2$ lie on a circle, namely $(C'_3)$), $Q_2, Q'_2, Q_3, Q'_3$ lie on a circle, namely $(C'_1)$); $Q_3, Q'_3, Q_1, Q'_1$ lie on a circle, namely $(C'_2)$). Let $(C_1) \cap C'_1) = A_1, A'_1$, $(C_2) \cap C'_2) = A_2, A'_2$, $(C_3) \cap C'_3) = A_3, A'_3$.

Then show that: Six points $A_1, A_2, A_3, A'_1, A'_2, A'_3$ lie on a circle

enter image description here

Community
  • 1
Oai Thanh Đào
  • 1,326
  • It was a little difficult to match the diagram with the text, since the $O_i$ circles are not labelled in the diagram. You might want to indicate that the black circles are the $O_i$, and the large blue points form the common axis. – Ted Jan 17 '17 at 10:13
  • @Ted I replaced by the new diagram – Oai Thanh Đào Jan 17 '17 at 10:32

1 Answers1

1

If $(O_1) \cap (O_2) \cap (O_3) = \{S, \, S^{*}\}$ just send $S^{*}$ to infinity by a Moebius transformation (e.g. an inversion) and without loss of generality, think that the three black circles $(O_1), \, (O_2), \, (O_3) $ are straight lines passing through a common point $S$. Then all the radical axes of all pair of circles from the set of three red and three green circles pass through the point $S$. This follows from grouping appropriate circles in triples and applying the radical axis theorem. Simply chase the relevant radical axes, apply say the power of point theorem each time, and all the statements follow from there.

Futurologist
  • 9,509