6

$$4\arctan\left({1\over \sqrt{\phi^3}}\right)-\arctan\left({1\over \sqrt{\phi^6-1}}\right)={\pi\over 2}\tag1$$ $\phi$;Golden ratio

I understand that we can use

$$\arctan{1\over a}+\arctan{1\over b}=\arctan{a+b\over ab-1}$$

that would take quite a long time and simplifying algebraic expressions involving surds is also difficult task to do.

How else can we show that $(1)={\pi\over 2}$?

gymbvghjkgkjkhgfkl
  • 8,090

4 Answers4

5

according to "How else can we show that"

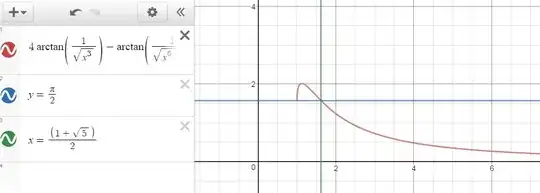
Take $f(x)=4\arctan\left({1\over \sqrt{x^3}}\right)-\arctan\left({1\over \sqrt{x^6-1}}\right)$ now you can show $f(1.618)=\dfrac{\pi}{2}$ enter image description here

This question is very interesting to me .I was working on $\phi $ properties ,like $\phi^2=\phi+1 \to \phi^3=\phi^2+\phi$ or $\psi=\dfrac{1}{\phi}$

we can see this $4\arctan\left({1\over \sqrt{\phi^3}}\right)-\arctan\left({1\over \sqrt{\phi^6-1}}\right)={\pi\over 2}$ as $4a-b=\dfrac{\pi}{2} $ so $4a=\dfrac{\pi}{2} +b \to \tan(4a)=-\cot(b)$ (if you prove this,prove the first relation) $$\phi=\dfrac{1+\sqrt5}{2} \\ \phi^3=\phi^2+\phi=(\dfrac{1+\sqrt5}{2})^2+(\dfrac{1+\sqrt5}{2})=\dfrac{1+5+2\sqrt5+2+2\sqrt5}{4}=\dfrac{8+4\sqrt5}{4}=2+\sqrt5 \to \\ \phi^6-1=(2+\sqrt5)^2-1=4+5+4\sqrt5-1=8+4\sqrt5$$ now redude to

$$4\arctan\left({1\over \sqrt{2+\sqrt5}}\right)-\arctan\left({1\over \sqrt{8+4\sqrt5}}\right)=\dfrac{\pi}{2} \to 4a-b=\dfrac{\pi}{2} \to \tan(4a)= ? -\cot(b)$$

$$\tan a=\dfrac{1}{\sqrt{2+\sqrt5}} \to tan 2a=\dfrac{2\tan a}{1-\tan^2a}=\\\frac{2\dfrac{1}{\sqrt{2+\sqrt5}}}{1-(\dfrac{1}{\sqrt{2+\sqrt5}})^2}=\dfrac{2\sqrt{2+\sqrt5}}{1+\sqrt5} \\ \tan(4a)=\dfrac{2\tan 2a}{1-\tan^22a}=\\\dfrac{2\dfrac{2\sqrt{2+\sqrt5}}{1+\sqrt5}}{1-(\dfrac{2\sqrt{2+\sqrt5}}{1+\sqrt5})^2}=\\ \dfrac{4\sqrt{2+\sqrt5}(1+\sqrt5)}{(1+\sqrt5)^2-4(2+\sqrt5)}=\\-2\sqrt{2+\sqrt5}$$ Other side we have $$-\cot b =-(\sqrt{8+4\sqrt5})=-2\sqrt{2+\sqrt5} \checkmark$$

Khosrotash
  • 24,922
  • 1
    During this ,I found an interesting relation $$\tan a=\dfrac{1}{\sqrt{2+\sqrt5}}=\dfrac{1}{\sqrt{\phi^3}} \to \tan 2a=\dfrac{2\tan a}{1-\tan^2a}=\\frac{2\dfrac{1}{\sqrt{2+\sqrt5}}}{1-(\dfrac{1}{\sqrt{2+\sqrt5}})^2}=\dfrac{2\sqrt{2+\sqrt5}}{1+\sqrt5}= \ \dfrac{\sqrt{2+\sqrt5}}{\dfrac{1+\sqrt5}{2}}=\dfrac{\sqrt{\phi^3}}{\phi}=\sqrt{\phi} $$ – Khosrotash Feb 05 '17 at 09:47
2

A detailed and autonomous prove (without reference to previous publication) :

enter image description here

JJacquelin
  • 66,221
  • 3
  • 37
  • 87
  • Very nice answer! I think there is a typo when you compute $\tan(\Phi)$: it should be $\tan(\Phi)=t\frac{16t^4+8t^2-7}{16t^4+16t^2-1}$. – Nicolas Feb 20 '17 at 23:09
  • @Nicolas : You are right. The denominator isn't $(16t^4+5t^2-7)$ but is $(16t^4+8t^2-7)$. Its value isn't $-\frac{11\sqrt{5}+1}{4}$ but is $-2(1+\sqrt{5})\neq 0$. Fortunately, the final result is the same. Thanks for the remark. – JJacquelin Feb 21 '17 at 06:42
  • You're welcome! – Nicolas Feb 21 '17 at 09:05
1

HINT: You can simplify a lot your equation working the identity $\phi^2=\phi+1$

Indeed

$\phi^3=\phi^2+\phi=2\phi+1$

and

$\phi^6-1=(2\phi+1)^2-1=4\phi^2+4\phi=4\phi^3$

Therefore your equation becomes

$ 4\arctan(a)-\arctan(a/2)=\frac{\pi}{2} $

with $a=\frac{1}{\sqrt{\phi^3}}$

Using the equality on arctan you provided should be enough to find the solution.

Maczinga
  • 1,117
  • 6
  • 12
0

Using $\phi^m=F_m\cdot\phi+F_{m-1}$ where $F_n$ is the $n$the Fibonacci Number.

Like Maczinga,

As $\phi^{3/2}>1,$ using showing $\arctan(\frac{2}{3}) = \frac{1}{2} \arctan(\frac{12}{5})$

$2\arctan\dfrac1{\phi^{3/2}}=\arctan\dfrac{2\phi^{3/2}}{\phi^3-1}=\arctan(\phi^{1/2})$

Again $\arctan\dfrac1{\sqrt{\phi^6-1}}=\arctan\dfrac1{2\phi^{3/2}}$

Now, $\arctan\phi^{1/2}-\arctan\dfrac1{2\phi^{3/2}}=\arctan\dfrac{\phi^{1/2}-\dfrac1{2\phi^{3/2}}}{1+\phi^{1/2}\cdot\dfrac1{2\phi^{3/2}}}$ $=\arctan\dfrac{2\phi^2-1}{\phi^{1/2}\cdot(2\phi+1)}$ $=\arctan\dfrac{2(\phi+1)-1}{\phi^{1/2}(2\phi+1)}$ $=\arctan\dfrac1{\phi^{1/2}}$

So, we are left with establishing $\arctan(\phi^{1/2})+\arctan\dfrac1{\phi^{1/2}}=\dfrac\pi2$

Community
  • 1
lab bhattacharjee
  • 274,582