A geometric construction related to an equidistributed sequence

Question

Context: I was reading a book when I encountered the following geometric construction in a chapter about equidistributed sequence.

Let's construct a series of $N$ points $A_1,\ldots,A_N$ of the plane, where $A_n$ has coordinates

$$\left(\mathrm{Re}\left(\sum_{k\leqslant n} e^{2\sqrt 2 i \pi k\log k}\right),\mathrm{Im}\left(\sum_{k\leqslant n} e^{2\sqrt 2 i \pi k\log k}\right)\right).$$

Then let's drawn the lignes $[A_n,A_{n+1}]$ for all $n\in\{1,\ldots,N-1\}$.

Here is what it looks for $N=200$, $N=1500$, $N=10^4$ and $N=10^5$ respectively.

My questions are the following.

• What is it behaving like this? What causes those spirals?

• Can we predict the coordinates of the center of each spiral?

• Can we predict for which value of $n$ $A_n$ will be at the center of a spiral?

Answer 1

I have had a number of experiences with these curlicue spirals, both by accident and by design. These are artifacts that accrue when a spiral equation is undersampled. But let's start at the beginning. Any curve in the complex plane can be expressed in terms of the arc length, $s$ by the equation

$$z=\int e^{i\int \kappa(s)ds}ds$$

where $\kappa(s)$ is the curvature. This equation is derived from the natural (or intrinsic) equation, which is independent of any coordinate system. For example, the relation between curvature and tangent angle, $\kappa(s)=d\theta/ds$, is a natural equation.

In your case we would idealize the spiral to the form

$$z(S)=\int_1^S e^{i2\sqrt{2}\pi s\ln s}ds$$

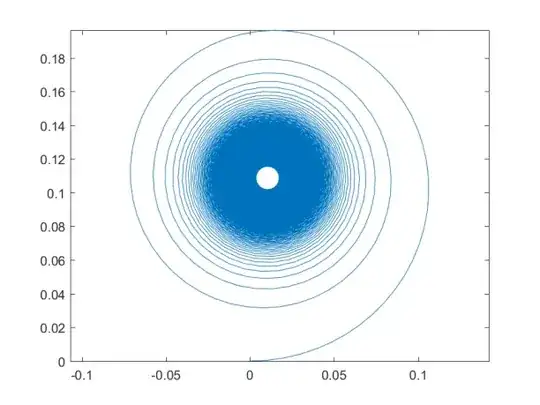
where we notice that we've taken the lower limit from $s=1$ to avoid problems with the logarithm, as well as to be consistent with your summation. A plot of $z(S)$ is shown in the first figure below and is seen the be similar to the right-hand-side of the Cornu/Euler spiral. Not surprising, because in that case you have $s\ln s \Rightarrow s^2$. As $S$ increases, the spiral is filled in with increasingly smaller loops.

However, excess curlicues can arise due to undersampling $s$ in the integral. What happens is that there are sudden changes in the integrand due to rapid changes in the sign of the sine/cosine terms, which throw the value of $z(S)$ out of the nominal spiral. It continues with another spiral until it is thrown off elsewhere.

In the limit of undersampling where $ds=1$, the result is identical with the summation in the OP, that is,

$$z(S)=\int_1^S e^{i2\sqrt{2}\pi s\ln s}ds=\sum_{k=1}^ne^{i2\sqrt{2}\pi k\ln k}=A_n$$

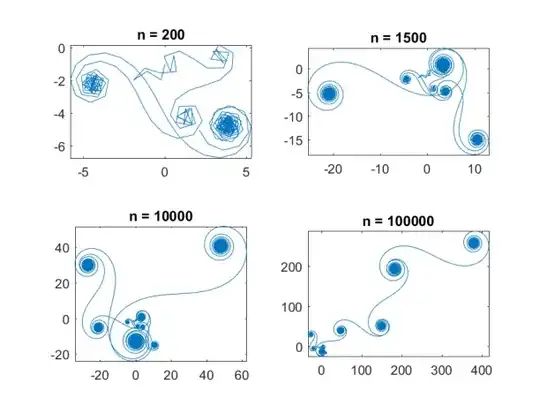
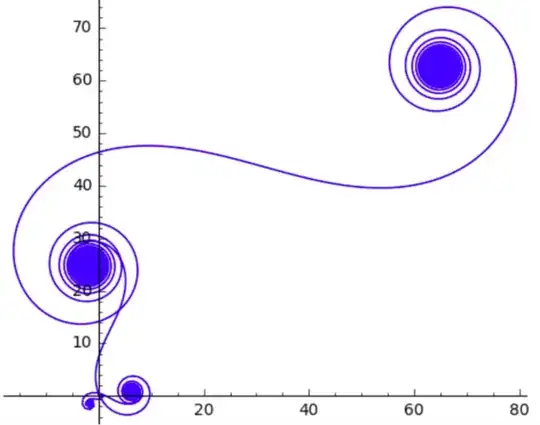
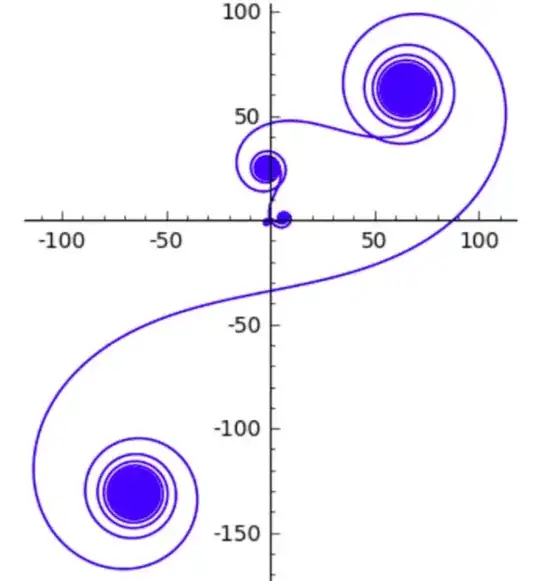
where $n=S$, of course. My results for $n=200,1500,10^4,10^5$ are shown in the second figure below. Since these are not in agreement with yours, I will tell you that these were calculated and plotted in the complex plane using Matlab and, in particular, using the the cumsum function, (i.e., cumulative summation). Notice that each image is a subset of the ones of lager values of $n$. In addition, these have been rotated by$-\pi/2$ for presentation purposes.

As to the question of predicting the centers of the spirals, I believe that it is highly unlikely. I cannot even determine that for the complete spiral because I cannot get a closed form solution to the integral. Moreover, I can't even get a numerical solution to the infinite integral (having tried WolframAlpha and Mathematica).

Finally, let me draw you attention to another to another post involving curlicue spirals where I also left an answer, Plotting exponential partial sums in the complex plane.