Plotting exponential partial sums in the complex plane

Question

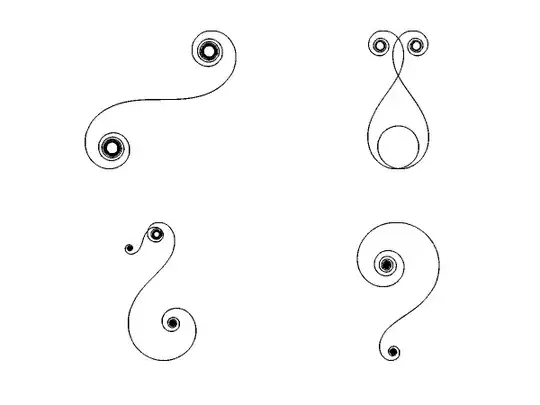
I was plotting the following sequence of points $(a_n)_{n = 0}^\infty$ in the complex plane for various reals $\alpha > 1$: $$a_n = \sum_{k = 0}^n e^{i k^\alpha}$$ I found that for many values of $\alpha > 1$ the path traced by $(a_n)$ displayed interesting nonrandom and even sometimes chaotic behaviour. The following images show the first few points, with successive points have increasing hue from red to purple (to red).

For $\alpha = 1.4$ we get:

As you can see there is a recurring pattern where the points in the sequence "spiral" around some attracting point for a while, before finally smoothly curving away into another spiral a few points later. The spirals also get larger as $n$ increases.

For $\alpha = 1.5$ we get mostly the same thing, just on a smaller scale:

For $\alpha = 2$ we get:

Here we have much the same pattern, except with considerable noise and there seems to only be two attracting points with the points oscillating between them.

The case for $\alpha = 2.25$ is particularly interesting:

The sequence starts off describing what looks like a random walk, but then eventually breaks into the same spiral pattern as previously, before resuming its random walk (actually, it does that several times at a smaller scale, but it's not visible here).

Finally it seems that for all sufficiently large $\alpha$, the sequence just becomes an uninteresting random walk without any (visible?) spirals.

---

Now I'm going to guess that this spiral pattern has something to do with the Euler Spiral, which appears in the Fresnel integrals which are really the continuous version of the sum above for $\alpha = 2$. But I don't see how to explain the patterns rigorously for $\alpha = 2$, let alone $\alpha \ne 2$. Does someone know how to relate my complex exponential sum to the Fresnel integrals somehow, or obtain some kind of argument for why we don't just get a random walk? After all, I would not expect $k^\alpha \bmod{2 \pi}$ to have any exploitable patterns at least in the limit, though I can see that the sequence $(a_n)$ could conceivably exhibit self-similarity.

Answer 1

The simple answer to your question is, yes: this has something to do with the Euler (or Cornu) spiral. You can almost see it in the figure with $\alpha=2$.

Working with the idea that your formulation is an approximation the integral, you can express a two-dimensional curve from the curvature as follows. I choose to use complex variables. The equation for the curve is given by

$$z(s)=\int e^{iP(s)} ds$$

where $\kappa (s)= P'(s)$, i.e., the derivative. For a more detailed description, please see my answer to a post on the Cornu spiral here: Is this Cornu spiral positively oriented or not?.

More generally, for exponents other than $\alpha=2$ we would be looking at Polynomial Spirals, say, $P(s)=\sum_{n=0}^N a_ns^n$, which frequently lead to these kinds of curlicue spirals. The principal reference for these is

Dillen, F. (1990). "The Classification of Hypersurfaces of a Euclidean Space with Parallel Higher Order Fundamental Form," Mathematische Zeitschrift, 203: 635-643.

My own efforts in this area are documented in Polynomial Spirals and the PDF file linked therein. Of course, mathematically, $P(s)$ is not limited to poynomials or anything else, for that matter.

And there are more discussions of curlicue spirals in

Stewart, Ian, *Another Fine Math You've Go Me Into", Chapter 12, The Thermodynamics of Curlicues, Dover.

The figure below shows two polynomial spirals from Dillen (top) and two of my own (bottom).