Solving $\tan(a+b)\tan(b+c)\tan(a+c)=1$

Question

I have a simple question : What are the condition on $a,b,c$ to have : $$\tan(a+b)\tan(b+c)\tan(a+c)=1$$ I think we can use the Huilier formula but I am not sure how to solve it. Thanks

Edit:

With : $\tan(a)\tan(b)<1$, $\tan(a)\tan(c)<1$, and $\tan(b)\tan(c)<1$.

My second idea would be to build a cyclic quadrilateral (convex in your case) with this formulas :

$\tan(\frac{\alpha}{2})\tan(\frac{\beta}{2})=\tan(\frac{\gamma}{2})\tan(\frac{\delta}{2})=1$

With $\alpha+\beta+\gamma+\delta=\pi$

On the other hand an other idea would be to use the semiperimeter :

For a cyclic quadrilateral with successive sides $a, b, c, d$ semiperimeter $s$, and angle A between sides $a$ and $d$,we have

$\tan(\frac{A}{2})=\sqrt{\frac{(s-a)(s-d)}{(s-b)(s-c)}}$

Answer 1

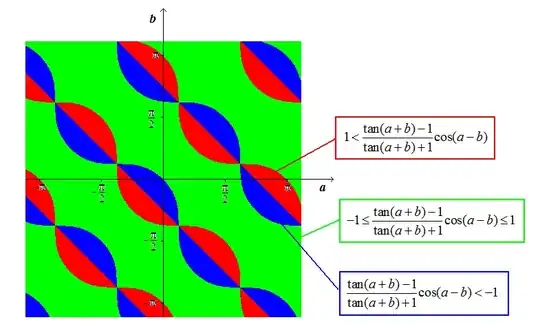
You are looking for the solutions to $$ \bbox[lightyellow] { \left\{ \matrix{ \tan \left( {a + b} \right)\tan \left( {a + c} \right)\tan \left( {b + c} \right) = 1 \hfill \cr \tan \left( a \right)\tan \left( b \right),\;\tan \left( a \right)\tan \left( c \right),\;\tan \left( b \right)\tan \left( c \right) < 1 \hfill \cr} \right. } \tag{1}$$

The equation is symmetric in $a,b,c$, and the solutions will be centered around the symmetric solution $$ \bbox[lightyellow] { a = b = c = \pi /8 } $$

This hints to try and make the substitution $$ \bbox[lightyellow] { \left\{ \matrix{ a + b = \pi /4 + \gamma \hfill \cr b + c = \pi /4 + \alpha \hfill \cr a + c = \pi /4 + \beta \hfill \cr} \right.\quad \Leftrightarrow \quad \left\{ \matrix{ a = \pi /8 + \left( { - \alpha + \beta + \gamma } \right)/2 \hfill \cr b = \pi /8 + \left( {\alpha - \beta + \gamma } \right)/2 \hfill \cr c = \pi /8 + \left( {\alpha + \beta - \gamma } \right)/2 \hfill \cr} \right. } \tag{2}$$

Making this change of variables we get, for $tan(a+b)$ $$ \bbox[lightyellow] { \tan \left( {a + b} \right) = \tan \left( {\pi /4 + \gamma } \right) = {{1 + \tan \gamma } \over {1 - \tan \gamma }} } \tag{3.a}$$ while for $tan(a)tan(b)$ we get $$ \bbox[lightyellow] { \eqalign{ & \tan a\tan b = \tan \left( {\pi /8 + \gamma /2 - \left( {\alpha - \beta } \right)/2} \right)\tan \left( {\pi /8 + \gamma /2 + \left( {\alpha - \beta } \right)/2} \right) = \cr & = {{\tan \left( {\pi /8 + \gamma /2} \right) - \tan \left( {\left( {\alpha - \beta } \right)/2} \right)} \over {1 + \tan \left( {\pi /8 + \gamma /2} \right)\tan \left( {\left( {\alpha - \beta } \right)/2} \right)}}{{\tan \left( {\pi /8 + \gamma /2} \right) + \tan \left( {\left( {\alpha - \beta } \right)/2} \right)} \over {1 - \tan \left( {\pi /8 + \gamma /2} \right)\tan \left( {\left( {\alpha - \beta } \right)/2} \right)}} = \cr & = {{\tan ^{\,2} \left( {\pi /8 + \gamma /2} \right) - \tan ^{\,2} \left( {\left( {\alpha - \beta } \right)/2} \right)} \over {1 - \tan ^{\,2} \left( {\pi /8 + \gamma /2} \right)\tan ^{\,2} \left( {\left( {\alpha - \beta } \right)/2} \right)}} \cr} } $$

and imposing the condition that $tan(a)tan(b)<1$ we get $$ \bbox[lightyellow] { \eqalign{ & \tan a\tan b < 1\quad \to \; \cr & \to \;\;\tan ^{\,2} \left( {\pi /8 + \gamma /2} \right) - \tan ^{\,2} \left( {\left( {\alpha - \beta } \right)/2} \right) < 1 - \tan ^{\,2} \left( {\pi /8 + \gamma /2} \right)\tan ^{\,2} \left( {\left( {\alpha - \beta } \right)/2} \right)\;\; \to \cr & \to \;\;\tan ^{\,2} \left( {\pi /8 + \gamma /2} \right)\left( {1 + \tan ^{\,2} \left( {\left( {\alpha - \beta } \right)/2} \right)} \right) < 1 + \tan ^{\,2} \left( {\left( {\alpha - \beta } \right)/2} \right)\;\; \to \cr & \to \;\;\tan ^{\,2} \left( {\pi /8 + \gamma /2} \right) < 1\;\; \to \cr & \to \;\; - 3\pi /4 < \gamma < \pi /4\quad \to \quad \tan \gamma < 1 \cr} } \tag{3.b}$$ and analogously for the other combinations.

So, the original equation is transformed into $$ \bbox[lightyellow] { \eqalign{ & \left\{ \matrix{ \tan \left( {a + b} \right)\tan \left( {a + c} \right)\tan \left( {b + c} \right) = 1 \hfill \cr \tan a\tan b,\;\tan a\tan c,\;\tan b\tan c < 1 \hfill \cr} \right.\quad \to \cr & \to \quad \left\{ \matrix{ a + b = \pi /4 + \gamma \hfill \cr b + c = \pi /4 + \alpha \hfill \cr a + c = \pi /4 + \beta \hfill \cr \left( {{{1 + \tan \alpha } \over {1 - \tan \alpha }}} \right)\left( {{{1 + \tan \beta } \over {1 - \tan \beta }}} \right)\left( {{{1 + \tan \gamma } \over {1 - \tan \gamma }}} \right) = 1 \hfill \cr - 3\pi /4 < \alpha ,\;\beta ,\;\gamma < \pi /4 \hfill \cr} \right.\quad \to \cr} } $$ $$ \bbox[lightyellow] { \to \quad \left\{ \matrix{ a = \pi /8 + \left( { - \alpha + \beta + \gamma } \right)/2 \hfill \cr b = \pi /8 + \left( {\alpha - \beta + \gamma } \right)/2 \hfill \cr c = \pi /8 + \left( {\alpha + \beta - \gamma } \right)/2 \hfill \cr 0 = \tan \alpha + \tan \beta + \tan \gamma + \tan \alpha \tan \beta \tan \gamma \hfill \cr \tan \alpha ,\;\tan \beta ,\;\tan \gamma < 1 \hfill \cr} \right. } \tag{4}$$

Conclusion

Equation (4) tells us that the solutions to (1) are reconducible to the roots of the symmetric polynomial $$ \bbox[lightyellow] { P(x,y,z) = x + y + z + xyz = x\left( {1 + yz} \right) + y + z } $$ which can be easily found by expressing one variable in terms of the other two, and which are rendered graphically by this plot.

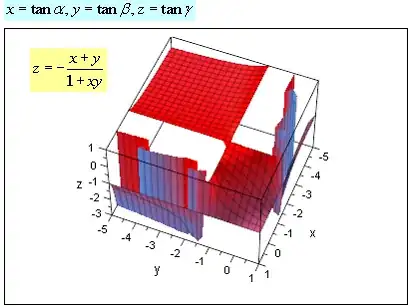
Note the similarity of the solution to the above with the addition formula for $\tanh$ $$ \bbox[lightyellow] { x = - {{y + z} \over {1 + yz}}\quad \leftrightarrow \quad - \tanh \left( {c + d} \right) = - {{\tanh c + \tanh d} \over {1 + \tanh c\tanh d}} } $$ which would deserve to be further expanded.

Otherwise, dividing by one of the variables taken to be non-null (e.g., $z$), the solutions are reconducible to the points on the hyperbola $$ \bbox[lightyellow] { h(\xi ,\eta ;z) = z^{\,2} \xi \eta + \xi + \eta + 1 = 0 } $$ and we can use the well developed apparatus of conic sections to analyze the behaviour of the solutions (existence, axes, canonical form, etc.) and to find appropriated parametric representations.

example :

In equation (4), choosing $\tan \alpha = 0,\,\;\tan \beta = 1/2$ we get $\tan \gamma = - 1/2 $, and then

$$ \bbox[lightyellow] { \eqalign{ & \tan \alpha = 0,\,\;\tan \beta = 1/2,\;\tan \gamma = - 1/2 \cr & \quad \quad \Downarrow \cr & \alpha = 0,\,\;\beta = \arctan \left( {1/2} \right),\;\gamma = - \arctan \left( {1/2} \right) \cr & \quad \quad \Downarrow \cr & \left\{ \matrix{ a = \pi /8 \hfill \cr b = \pi /8 - \arctan \left( {1/2} \right) \hfill \cr c = \pi /8 + \arctan \left( {1/2} \right) \hfill \cr} \right. \cr & \quad \quad \Downarrow \cr & \tan \left( {a + b} \right)\tan \left( {a + c} \right)\tan \left( {b + c} \right) = \cr & = \tan \left( {\pi /4 - \arctan \left( {1/2} \right)} \right)\tan \left( {\pi /4 + \arctan \left( {1/2} \right)} \right)\tan \left( {\pi /4} \right) = \cr & = {{1 - 1/2} \over {1 + 1/2}}{{1 + 1/2} \over {1 - 1/2}} = 1 \cr} } $$

addendum

The similarity with the addition formula for $\tanh$ provides in fact an interesting parametric equation for $a,b,c$ in terms of $u,v$, which
for $-\infty<u,v<\infty$ always satisfies the original system (1) $$ \bbox[lightyellow] { \left\{ \matrix{ a = \pi /8 + \left( { - \alpha + \beta + \gamma } \right)/2 \hfill \cr b = \pi /8 + \left( {\alpha - \beta + \gamma } \right)/2 \hfill \cr c = \pi /8 + \left( {\alpha + \beta - \gamma } \right)/2 \hfill \cr \alpha = \arctan \left( {\tanh u} \right) \hfill \cr \beta = \arctan \left( {\tanh v} \right) \hfill \cr \gamma = \arctan \left( {\tanh \left( { - u - v} \right)} \right) = - \arctan \left( {\tanh \left( {u + v} \right)} \right) \hfill \cr} \right. } \tag{5}$$

In fact, we have $$ \bbox[lightyellow] { \left. {\left\{ \matrix{ 0 \equiv \tan \alpha + \tan \beta + \tan \gamma + \tan \alpha \tan \beta \tan \gamma \; \hfill \cr \tan \alpha ,\;\tan \beta ,\;\tan \gamma < 1\; \to \;\left\{ \matrix{ \tanh u,\;\tanh v < 1 \hfill \cr - 1 < \tanh \left( {u + v} \right) \hfill \cr} \right. \hfill \cr} \right.\quad } \right|\; - \infty < u,v < \infty } $$

Answer 2

By expansion, we get

$$\frac{(\tan(a)+\tan(b))(\tan(b)+\tan(c))(\tan(c)+\tan(a))}{(1-\tan(a)\tan(b))(1-\tan(b)\tan(c))(1-\tan(c)\tan(a))}$$

And as you wrote the multiplication of the terms $\tan(a)\tan(b)<1$ and so on therefore, the denominator is always less than $1$ and hence the whole terms are greater than one. So all the terms $\tan(a+b)\tan(b+c)\tan(c+a)$ have to be $1$. So, $$\tan(a+b)=\tan(b+c)=\tan(c+a)=1$$.

Answer 3

$$\tan(a+b)\tan(b+c)\tan(a+c)=1 \tag 1$$ $$\tan(b+c)\tan(a+c)=\frac{\cos(b-a)-\cos(b+a+2c)}{\cos(b-a)+\cos(b+a+2c)}$$ $$\tan(a+b)\frac{\cos(b-a)-\cos(b+a+2c)}{\cos(b-a)+\cos(b+a+2c)}=1$$ This can be solved for $\cos(b+a+2c)$ $$\cos(b+a+2c)=\frac{\tan(a+b)-1}{\tan(a+b)+1}\cos(a-b)$$ $$c=\frac{1}{2}\left(-a-b+\cos^{-1}\left(\frac{\tan(a+b)-1}{\tan(a+b)+1}\cos(a-b) \right) \right) \tag 2$$ If we chose arbitrary values of $a$ and $b$, Eq.(2) gives $c$ so that Eq.(1) is satisfied. But $c$ can be complex. To obtain $c$ real, the condition is : $$-1\leq \frac{\tan(a+b)-1}{\tan(a+b)+1}\cos(a-b) \leq 1$$

On the graph, the areas allowed for $(a,b)$ to achieve $c$ real are drawn in green. The whole is periodic as expected.

NUMERIAL EXAMPLE :

For example, $a=0.2$ and $b=0.75$

$\frac{\tan(a+b)-1}{\tan(a+b)+1}\cos(a-b)\simeq 0.141608$

$c=\frac{1}{2}\left(-a-b+\cos^{-1}\left(\frac{\tan(a+b)-1}{\tan(a+b)+1}\cos(a-b) \right) \right)\simeq 0.239355$

$\tan(a+b)\tan(b+c)\tan(a+c)\simeq 1.000000$

$\cos^{-1}$ is multi-valuated. Other convenient values of $c$ are obtained, for example $c\simeq 1.952237$

Of course, a numerical example isn't a proof. The analytic proof is above. This shows that one can obtain an infinity of solutions with the above method.