I am trying to determine whether the $\alpha$ sublevel sets of functions of the form $f(x_1,x_2) = x_1x_2$ and $f(x_1,x_2) = \frac{1}{x_1x_2}$ are convex or not. For one dimensional examples, I can draw the graph and more or less see whether the set is convex or not. For these examples, however, is there any way to show whether they are convex or not?
1 Answers
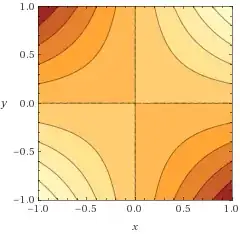
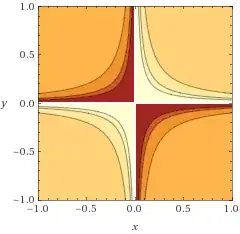
You can get intuition in 2D using the same approach: draw contour plots of the function over the plane and look at the shape of the level sets. For example, using Wolfram Alpha I get for your two functions (darker = more negative):
Here we see clearly that for the first function, the sublevel sets are in "two disconnected pieces" when $\alpha<0$ and so cannot be convex; similarly when $\alpha>0$ the sublevel set is in one piece, but still not convex since in the upper-right or bottom-left quadrant you can draw a line segment that "cuts" through a region more positive than $\alpha$. Similarly you can inspect the shape of the sublevel sets of the second function and see that they are never convex.
Of course, to prove that these regions are convex, you would need to show that for any two points $(x_1,y_1)$ and $(x_2,y_2)$ with
- $f(x_1,y_1) \leq \alpha$
- $f(x_2,y_2) \leq \alpha$,
and for any $t\in(0,1)$,
$$f[(1-t)x_1 + tx_2, (1-t)y_1 + ty_2] \leq \alpha.$$
Or to prove that the regions are not convex, you will need to exhibit for each $\alpha$ a specific counterexample $(x_1,y_1,x_2,y_2,t)$.
The pictures should let you easily figure out how to construct suitable counterexamples.
- 49,280