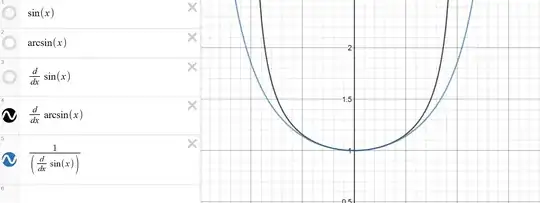
I was trying to find the derivative of $$\arcsin(x) = \sin^{-1}(x)$$
I thought that I could use the rule of inversion:
$$({f^{-1}})'(x) = \dfrac{1}{f(x)'}$$
Therefor the derivative of $\arcsin(x)$ should be: $$\dfrac{1}{\cos(x)}$$
But for some reason, this seems to only work for small $x$. Where did I do a mistake?
Greetings, Finn
Because the rule is$$(f^{-1})'(x)=\frac1{f'\bigl(f^{-1}(x)\bigr)}$$and therefore\begin{align}\arcsin'(x)&=\frac1{\cos\bigl(\arcsin(x)\bigr)}\\&=\frac1{\sqrt{1-\sin^2\bigl(\arcsin(x)\bigr)}}\\&=\frac1{\sqrt{1-x^2}}.\end{align}
with $$sin(y)=x$$ we get $$\cos(y)\frac{dy}{dx}=1$$ so $$\frac{dy}{dx}=\frac{1}{\cos(y)}$$ therefore $$\frac{dy}{dx}=\frac{1}{\sqrt{1-x^2}}$$
In fact, we have
$ (\arcsin x)' = \dfrac{1}{\sqrt{1-x^2}}$
since,$(f^{-1}(x))' = \dfrac 1{f'(y)}$
You could use the correct formula of inversion: $$(f^{-1})'(x)=\frac 1{f'\bigl(f^{-1}(x)\bigr)}.$$ In other words, if you set $y=f^{-1}(x)$, then $$(f^{-1})'(x)=\frac 1{f'(\color{red}{y})}.$$ Here you obtain $$\arcsin' x=\frac1{\cos(\arcsin x)}=\frac1{\sqrt{1-x^2}},$$ because of Pythagoras' identity and $-\frac\pi2\le\arcsin x\le \frac\pi2$, so the cosine is $\ge 0$.
It can be easier to apply the definition of arcsine: $$ x=\sin(\arcsin(x)) $$ The “rule of inversion” ensures you that the derivative of the arcsine exists (with a condition that I'll deal with later) so you can differentiate both sides using the chain rule: $$ 1=\cos(\arcsin(x))\arcsin'(x) $$ Therefore $$ \arcsin'(x)=\frac{1}{\cos(\arcsin(x))} $$ The condition I mentioned above is, of course, that $\cos(\arcsin(x))\ne0$.
Now we just have to simplify $\cos(\arcsin(x))$; use the fact that $\arcsin(x)\in[-\pi/2,\pi/2]$, so $$ \cos(\arcsin(x))=\sqrt{1-\sin^2(\arcsin(x))}=\sqrt{1-x^2} $$ Thus $$ \arcsin'(x)=\frac{1}{\sqrt{1-x^2}}\qquad x\in(-1,1) $$
