What is the relationship between blue area and red area?

Question

This is a grade school problem!

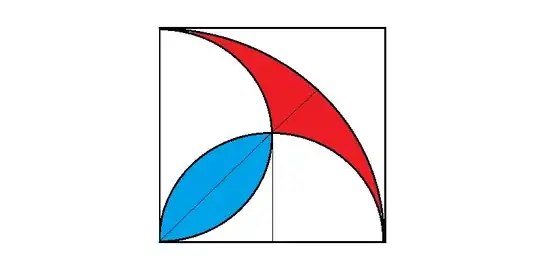
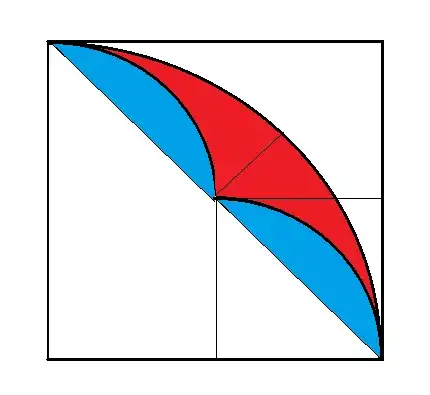
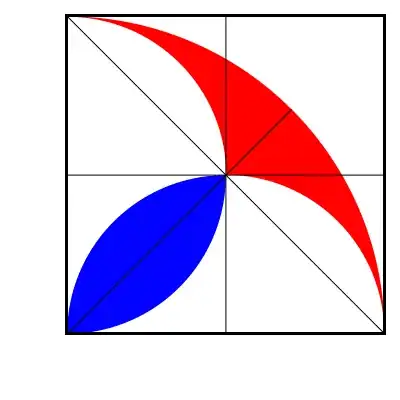
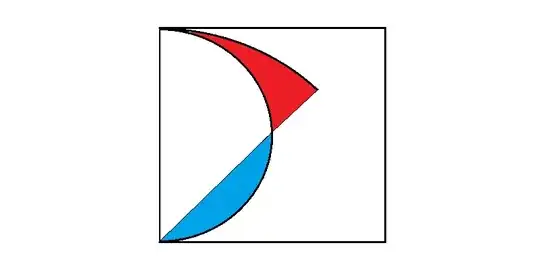
Consider the following figure:

It is very easy to show that the red area and the blue area equal. I can demonstrate this based on my knowledge related to the computation of the surface areas of circular sectors and triangles. Both areas equal $2\left(\frac{r^2\pi}4-\frac{r^2}2\right)$ where $r$ is the radius of the smaller circles.

But, how am I going to show the same if I forget, for good, the formula providing the area of a triangle?

I am not able to get rid of my thought process using triangles.

Do you mean how to show that they are equals or to derive the expression? — user, Mar 19 '18 at 10:55
@KingTut: Sorry, I forget to mention that this is a 7th grader problem. No homtety, no integration etc. — zoli, Mar 19 '18 at 10:58
@KingTut take a look here https://en.wikipedia.org/wiki/Homothetic_transformation Ican't make a sketch now but the idea is to consider the big quarter of circle abd the small one — user, Mar 19 '18 at 11:02
@zoli anyway homothety is just an elementary concept, are you sure it can't be used at a grade level. For instance $A(L)=L^2 \implies A(2L)=(2L)^2=4L^2$ is just a trivial algebra fact. — user, Mar 19 '18 at 11:05
If you forbid homothety, then you mustn't use $\pi r^2$ in your calculation, either! You know, the proportionality 'Area ~ Radius Squared' follows from homothety! — CiaPan, Mar 19 '18 at 13:59
@CiaPan Its not at all required as I said in my answer also. you can use similarity, same as you did to get the first equation in your answer! "$.. = 4$". — King Tut, Mar 19 '18 at 14:42
@KingTut Similarity is a homothety ...plus rotation and possibly line symmetry (in a plane; to be replaced with mirroring in 3D, and so on). — CiaPan, Mar 19 '18 at 14:51
@KingTut Yes. But OP didn't define that constraint in the problem description. It has been added in comments above, and I have read it some time after posting my answer. I have no idea how to get to the required answer without such basic geometric facts. It's all about proportions of lengths and areas during scaling, and that IS homothety (or more general similarity). Even square area = side×side follows from it...! — CiaPan, Mar 19 '18 at 15:08

score 50 · Answer 1 · edited Mar 20 '18 at 05:53

50

See the image with blue parts shifted:

The single blue figure is the same part of its small square as the red plus both blue of the big square, hence areas $$\frac{2\cdot blue + red}{blue}=\frac{big\ square}{small\ square}=4$$ so $$2\cdot blue + red = 4\cdot blue$$ hence $$red = 2\cdot blue$$ Q.E.D.

Without the formula for the area of a triangle, and without the formula for the area of a circle...

edited Mar 20 '18 at 05:53

heropup

135,869

answered Mar 19 '18 at 11:22

CiaPan

13,049

Very nice! .... – Bram28 Mar 19 '18 at 12:04
Yeah I like this thinking! – King Tut Mar 19 '18 at 13:23
@CiaPan: Thank you for your great answer. The number of up votes (mine is there) expresses the value. – zoli Mar 19 '18 at 22:54
7

I took the liberty of adding an animation to illustrate the relationship between the shaded regions. – heropup Mar 20 '18 at 05:54
7

Nice animation, how did you make it @heropup – King Tut Mar 20 '18 at 06:26
@heropup Amazing! :) Thank you! – CiaPan Mar 20 '18 at 07:54

score 12 · Accepted Answer · edited Mar 20 '18 at 17:28

12

There are two red parts and two blue parts. Let one blue part be called $B$ and red be $R$. Radius of small circle be $r$. Now write area of big quarter circle with radius $2r$ in terms of these variables using inclusion exclusion principle:

$$2 \cdot \frac{\pi r^2}{2} -2B+2R = \frac{\pi (2r)^2}{4}\\ R=B$$

Note: We actually do not need that area of a disk is $\pi r^2$. We can assume it to be $A$ and use similarity of figures.

$$2 \cdot \frac{A}{2} -2B+2R = \frac{2^2A}{4} \\ R=B$$

edited Mar 20 '18 at 17:28

Yakk

1,431

answered Mar 19 '18 at 11:04

King Tut

3,074

but we need to show that B=R. – user Mar 19 '18 at 11:06
@gimusi RHS is area of big quarter circle – King Tut Mar 19 '18 at 11:07
Isn't it $2\pi r^2-2B+2R=4\pi r^2$? – DynamoBlaze Mar 19 '18 at 11:11
@KingTut that's fine! Even if it is precisely equivalent to apply homothety but without mention that. (+1) – user Mar 19 '18 at 11:12
@gimusi Oh i wasn't aware of that at all! I will try to learn what it is.. – King Tut Mar 19 '18 at 11:14
@KingTut: I feel stupid, thx. – zoli Mar 19 '18 at 11:15
Free downvote without a reason. – King Tut Mar 19 '18 at 15:18
@malay no it's not and please check your calculation. The answer was correct even in the first edit. – King Tut Mar 20 '18 at 05:28

Michael Hoppe · Answer 3 · 2018-03-19T21:54:03.257

11

Apply the carpet theorem, see https://www.cut-the-knot.org/Curriculum/Geometry/CarpetsInSquare.shtml. Consider the upper eighth of the big circle and the left halve circle. Since their areas are equal, the areas which are not covered by both must be equal as well, that is the upper half of the red area equals the lower half of the blue one.

edited Mar 19 '18 at 21:54

answered Mar 19 '18 at 11:20

Michael Hoppe

18,103
3
32
49

1

Please see the image I added – I hope it reflects your description. – CiaPan Mar 19 '18 at 15:16
To put it another way, a circle of radius 1 has the same area as 4 circles of diameter 1. – Joce Mar 19 '18 at 15:34
@CianPan. Well done, thank you very much. – Michael Hoppe Mar 19 '18 at 17:44
@joce that's the fact all answer here, all of them because I think it's not possible without it. – King Tut Mar 20 '18 at 02:53
Isn't that a right halve circle? (admittedly on the left) :) – Yakk Mar 20 '18 at 17:50
@CiaPan It woudl be clearer if you used different colors to outline the 1/2 circle and the larger 1/8 circle, or some other indication. – Yakk Mar 20 '18 at 17:51
@Yakk I didn't use any colors – I used a rubber only. This is exactly the original image from the questions, I just removed some parts of it. – CiaPan Mar 21 '18 at 14:59

score 5 · Answer 4 · answered Mar 19 '18 at 18:25

If you forgot formulas, but remember that areas are quadratic (i.e. "double the length, quadruple the area"), then you know that a circle of radius $2r$ uses four times the area of circle of radius $r$. Here, you have one quarter of a circle of radius $2r$, and one circle of radius $r$ (in two halves), so they should cover the same area. In other words, the two halves of the small circle should be enough to cover the large quarter circle.

However, the two halves of the small circle overlap (the blue area) and thus some of the area covering power is lost. And, indeed, the big quarter-circle is partially uncovered (the red area). Therefore, the blue and red area MUST be equal.

mbomb007 · Answer 5 · 2018-03-19T15:36:52.523

2

The red area $R$ is the area of the big quarter circle minus the internal white and blue areas. The radius of the larger circle is 2*r. So the area of the big quarter circle is:

$$ Q = \frac {\pi(2r)^2}{4} = \pi r^2 $$

Visually, this is equivalent to a quarter of each small circle (together, these are half a small circle) plus $r^2$ (the area of the small square in the lower-left corner) plus the red area:

$$ Q = \pi r^2 = \frac {\pi r^2}{2} + r^2 + R $$

Therefore:

$$ R = \frac {\pi r^2}{2} - r^2 $$

The blue area is equal to the area of the small square $r^2$ minus 2 times a smaller unknown white area, which we will call $S$. $S$ is equal to the area of the small square minus a quarter of the small circle.

$$ B = r^2 - 2S $$

$$ S = r^2 - \frac {\pi r^2}{4} $$

Simplify:

$$ B = r^2 - 2 \cdot (r^2 - \frac {\pi r^2}{4}) $$

$$ B = r^2 - 2r^2 + \frac {\pi r^2}{2} $$

$$ B = \frac {\pi r^2}{2} - r^2 $$

edited Mar 19 '18 at 15:36

answered Mar 19 '18 at 15:19

mbomb007

139

(I think you can immediately say "$S$ is equal to the area of the small square, minus one quarter of the small circle.") – mathmandan Mar 19 '18 at 15:29
@mathmandan Ah, yes, that's nice. I was just saying how I visualized it, but that is just as clear to see by looking at the picture. – mbomb007 Mar 19 '18 at 15:35
Sure, and you have a nice solution either way. See you around at PPCG, and thanks for contributing here as well! – mathmandan Mar 19 '18 at 16:05

score 2 · Answer 6 · answered Mar 19 '18 at 19:29

I assume the sides of the square are $2R$, and that the blue area is the area of the intersection of two half circles of radius $R$

$RedArea = Sa_{Big_{quartercircle}} - 2 * Sa_{Small_{halfcircles}} + intersection $

But

$Sa_{Big_{quartercircle}} = \pi R^2$

and:

$Sa_{Small_{halfcircle}} = \pi R^2\div 2$

So:

$RedArea = intersection = BlueArea$

score 1 · Answer 7 · answered Mar 19 '18 at 17:33

Let r = the radius of the large quarter-circle = the side of the square. \ Area of the big quarter-circle = (\pi * r^2) / 4 \ Area of two smaller semi-circles = (\pi * r^2) / 4 \ These two areas are equal. \ Graphically, the area of the big quarter-circle (\pi * r^2) / 4 = area of two smaller semi-circles (\pi * r^2) / 4 + red shaded area (because it is contained outside the smaller circles) - blue area (because it is contained by the smaller circles twice). \ Cancel the circle areas on each side. 0 = blue area - red area \ Use addition to move the red area to the left side. red area = blue area

What is the relationship between blue area and red area?

7 Answers7

Linked