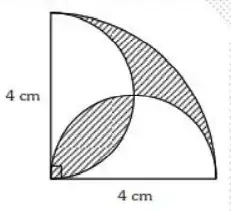
First I calculate the area of 1/4 circle, that is $\frac{1}{4}\pi.r^2=\frac{1}{4}\pi.4^2=4\pi.$
Then I know the area of each 1/2 circles inside the 1/4 circle is $\frac{1}{2}\pi.2^2=2\pi.$ But I know it's not as simple as 1/4 circle $-$ 1/2 circles inside. I'm having a hard time determining the shaded area that is the intersection of two 1/2 circles inside. Any idea of the steps for this solution? Thanks in advance.
I think this method would help you.
I learned a similar problem at school before.
Let origin $O(0,0)$ be the center of quarter circle (as shown in the figure). Now we have following equations of quarter and semi-circles $$x^2+y^2=16$$ $$x^2+(y-2)^2=4$$ $$(x-2)^2+y^2=4$$
It's worth noticing that the straight line $y=x$ divides the required area into two equal parts. Therefore the total required area is twice the area of one part under $y=x$ which is twice the sum of areas $A_1, A_2$ & $A_3$ (as shown in above figure) given as follows $$2(A_1+A_2+A_3)=2\left(\int_0^2\left(x-\left(2-\sqrt{4-x^2}\right)\right)dx+\int_2^{2\sqrt2}\left(x-\sqrt{4-(x-2)^2}\right)dx+\int_{2\sqrt2}^4\left(\sqrt{16-x^2}-\sqrt{4-(x-2)^2}\right)dx\right)$$ (Rearranging the terms) $$=2\left(\int_0^{2\sqrt2}xdx+\int_0^2(\sqrt{4-x^2}-2)dx+\int_{2\sqrt2}^4\sqrt{16-x^2}\ dx-\int_{2}^4\sqrt{4-(x-2)^2}dx\right)$$ $$=2\left(\left[\frac{x^2}{2}\right]_0^{2\sqrt2}+\left[\frac x2\sqrt{4-x^2}+2\sin^{-1}\left(\frac x2\right)-2x\right]_0^2+\left[\frac x2\sqrt{16-x^2}+8\sin^{-1}\left(\frac{x}{4}\right)\right]_{2\sqrt2}^4-\left[\frac{(x-2)}{2}\sqrt{4-(x-2)^2}+2\sin^{-1}\left(\frac{x-2}{2}\right)\right]_{2}^4\right)$$ $$=2\left(4+\pi-4+4\pi-4-2\pi-\pi\right)$$ $$=4\pi-8$$
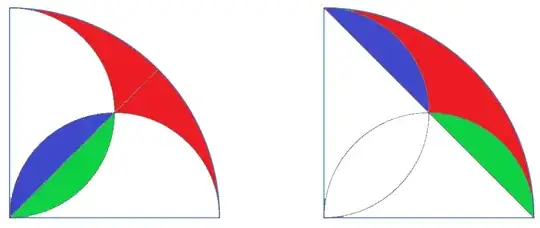
Let $A_1$ and $A_2$ denote the circular segment of the circle of radius $r_1 = 4\ \mathrm{cm}$ and $r_2 = 2\ \mathrm{cm}$, respectively, from $\theta = 0\ \mathrm{rad}$ to $\pi / 2\ \mathrm{rad}$.
We see that the convex shaded shape has the area of $2 A_2$, and that the other shaded shape has the area of $A_1 - 2 A_2$. Hence the total area is $A_1$.
