3

I'm working on a problem in which the random variable is the difference between two random variables. We know from math that the mean will be the difference of the means, and that the variance will be the sum of the variances. I know that for a Poisson distributions the sum of two independent variables will be another Poisson distribution with mean the sum of the means, and this will be identical to the variance.

Therefore I can treat the difference between Poisson distributed random variables the same way. However, a Poisson distribution has only positive values, and I know that the difference between the random variables will have some value that turns out to be negative. What am I missing?

David G. Stork
  • 29,774
gciriani
  • 424

1 Answers1

5

Here are two Poisson distributions:

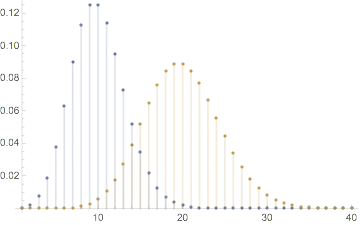
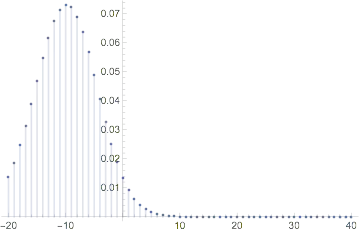
enter image description here

Here is the associated Skellam Distribution (which is the solution to your problem):

enter image description here

Indeed, the distribution is defined for negative values. Moreover, the mean of the Skellam distribution is the difference of the means of the two Poisson distributions (even if that value is negative) and the variance of the Skellam distribution is the (positive) sum of the variances of the Poisson distributions.

David G. Stork
  • 29,774
  • Thank you for answering! Does it apply to a continuous distribution?

    The Wikipedia article on the Skellam distribution states that it is a discrete probability distribution. However, I'm trying to model a game of bocce: I assume the distance of each player's bowl from the jack is Poisson distributed, and it is a continuous variable. So, I'm wondering if the Skellam distribution would be a correct application, since the article says discrete and not continuous variable. The area under the curve, on the positive side would be the probability of the ball of one player to be closer to the jack.

     – gciriani Sep 29 '18 at 18:45
  • You said Poisson (which is discrete) and nothing whatsoever about continuous. Skellam is thus also discrete. I would just focus on discrete, with very small increment size. – David G. Stork Sep 29 '18 at 20:57