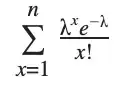0

I've got two variables A and B with ≤ following a Poi(), resp. Poi() distribution.

Given values a1 and b1 we can figure out if these particular values are significantly decreased by calculating the probability of getting a1 and b2 or lower number:

enter image description here

where n=a and n=b, = and = b accordingly for each variable.

If the probability of getting a1(or b1) or lower value <5% threshold we can say that this particular value significantly decreased.

My question is how can we figure out the answer to the same question for variable C := A/B (so it is between 0 and 1). If we have got the value of c1 = a1/b2 then how do we know if c1 significantly decreased?

user912830823
  • 117

1 Answers1

1

I suggest that, instead of $C:=A/B$, you consider random variable:

$$C:=B-A$$

In particular $C$ should be (or tested to be) Poisson-distributed with a parameter that you will call $\lambda c$. You should get $c:=b-a$ due to a version of the additive property of Poisson random variables. In this case, "significantly less" could be translated into "$C$ takes comparatively high values".

Remarks :

1) if sometimes $A > B$, you have no longer a Poisson distribution ; see in this case (Distribution of difference between independent Poisson random variables).

2) If you aren't convinced that it is better to study the difference, and keep trying to study the quotient $C:=A/B$, here is a reference that can be of interest.

Edit : following our exchanges, if $C$ is defined by $C=B-A$, i.e. $B=A+C$, therefore $A/B=A/(A+C)=1/(1+C/A)$, I have done a simulation of Random Variable $R=A/B=1/(1+C/A)$ (see below)

enter image description here

Taking $A$ and $C$ both Poisson with resp. parameters $\lambda=20$ and $\lambda=25$, we obtain a rather gaussian distribution. Here is the Matlab program that has generated this histogram:

function ratpoi;
for q=1:100000
   A=poi(20);C=poi(25);
   T(q)=1/(1+C/A); 
end;
hist(T,30);

function P=poi(L); % gen. Poisson Rand. Var. with par. L
EL=exp(-L);k=0;p=1;
while p>EL
    p=p*rand;k=k+1;
end
P=k-1;
Jean Marie
  • 81,803
  • 1
    hi @Jean Marie and thanks for your answers and corrections! I corrected my answer based on that so (hopefully) its easier to see what im after. Im trying to figure out if we have variable that is C := A/B then how can we say that particular value c1 = a1/b1 significantly decreased? Im suspecting C is no plonger Poisson distributed? – user912830823 Sep 25 '19 at 06:45
  • I still don't understand what you mean by "decreased" ... Do you mean "small" or "small with respect to..." ? – Jean Marie Sep 25 '19 at 06:48
  • Let's say my λa=50, and value of a1 = 33, im trying to figure out what are the probability of getting a1 or lower given λa. I do this using the formula in the question. If the probability is 5% or lower i assume it is a significant decrease. Here are more details on that: https://math.stackexchange.com/questions/3341960/poisson-distribution-for-large-numbers/3341970?noredirect=1#comment6878863_3341970 – user912830823 Sep 25 '19 at 06:53
  • I understand a little better. You should have given this reference at first in your question. Besides, saying that you have two Poisson random variables such that $A \leq B$ without explaining more is not correct (and will introduce flaws in any further reasoning) unless you explain why and how $A$ is linked with $B$. This is why it is so natural to introduce $A$ and $C$ (both Poisson with different parameters) and then define $B=A+C$, wich guarantees that $A \leq B$. – Jean Marie Sep 25 '19 at 07:02
  • (ctd) in this way, you will have to study $A/B=1/(1+C/A)$ where $A$ and $C$ are both Poisson distributed. – Jean Marie Sep 25 '19 at 07:05
  • i see thanks! Also, i probably should've mentioned that A and B are a different kind of variables, ie A is orders and B is clicks - doest it still make sense defining B = A+C? And if so given /=1/(1+/) how can i say that a1/b1 significantly decreased? It is not poisson distributed anymore or is it? – user912830823 Sep 25 '19 at 07:18
  • See my edit answering your question. – Jean Marie Sep 26 '19 at 16:58