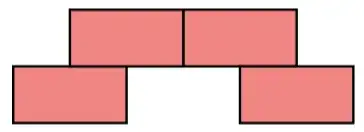
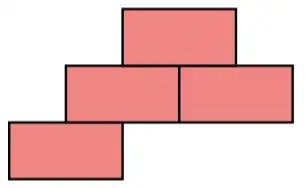
Suppose you stack $n$ LEGO bricks ($2 \times 1$) in a plane, where
- The base is contiguous
- Each level is offset from the level below it by one stud.
- Bricks are only stacked on top of other bricks, not below.
It turns out that there are exactly $3^{n-1}$ such stacks. (See here beginning on page 25.)
Question
How many such stacks are left-right symmetric? By my brute force program:
n | # symmetric stacks
---+-------------------
1 | 1
2 | 1
3 | 3
4 | 3
5 | 7
6 | 9
7 | 19
8 | 25
9 | 53
10 | 71
11 | 149
12 | 203
13 | 423
14 | 583
15 | 1209
And by a parity argument, there are an odd number of such stacks for each value of $n$.
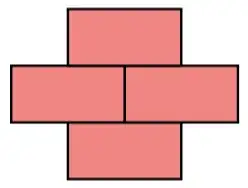
Examples
For example, the following three stacks of four bricks are legal:
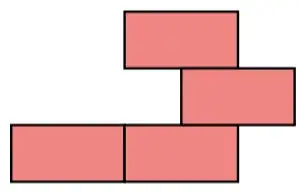

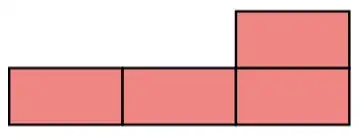
Non-Examples
The following three stacks are not legal because they violate the three conditions above: in the first, the base is not contiguous; in the second, the levels are not offset; and in the third, the second brick in the second row doesn't have any bricks below it.