14

Suppose that you have a stack of identical, frictionless, uniform-density $1 \times 2$ bricks arranged in the ordinary configuration (each row is offset by $1$ relative to the row below.)

Question

Is there a combinatorial rule that captures whether or not a given stack of bricks would be stable? In particular, that no small vertical force will cause the stack to move.

In other words, how can one determine whether or not a configuration is stable without doing a static force analysis.

(Admittedly, this question is a little hand-wavey, so let me know if I can clarify anything.)

Examples

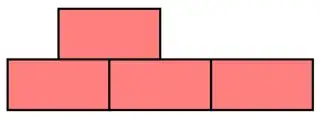
Clearly, a stack of bricks that does not have any "overhangs" should be stable:

Stack without overhangs

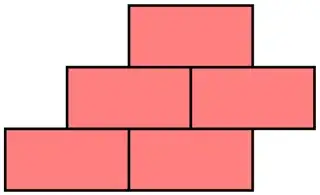
But we can also allow a cantilever if there's a brick above:

Valid cantilever

Non-examples

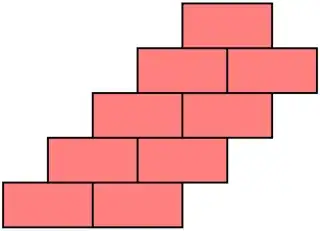
However, having a brick above is not sufficient, because a stack like this should not be stable.

Invalid cantilever

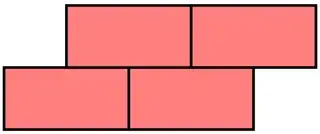
Similarly, having a brick above is necessary because a configuration like this is in unstable equilibrium; in particular the upper-right brick in this example would fall if an arbitrarily small force were applied to the right side.

Unstable equilibrium

Community
  • 1
Peter Kagey
  • 5,052
  • 1
    The best I can do is enumerate total brick stacks of $n$ bricks, both stable and unstable. Surprisingly, the result is quite simple considering the difficulty of the problem. There are $3^{n-1}$ total brick stacks. – N. Shales Apr 11 '18 at 01:20
  • On the Code Golf Stack Exchange, there was a related puzzle—but it didn't obey Newtonian mechanics. https://codegolf.stackexchange.com/q/38548/53884 – Peter Kagey Apr 11 '18 at 15:49
  • @N.Shales, I enumerated a few cases by hand, and I believe you—but how do you prove this? – Peter Kagey May 04 '18 at 20:57
  • It is possible to construct a 'brick tower' from irreducible parts. The sequence of these parts can be formed using a generating function. It's quite difficult to explain without diagrams. The irreducible parts are called "pyramids" and "half-pyramids". A pyramid has a base of 1 brick and bricks on top to the left and right, half-pyramids only have bricks on top to the right. A 'brick tower' is always formed by 1 pyramid on the left and any number of subsequent half-pyramids successively to the right. – N. Shales May 04 '18 at 22:32
  • See here beginning on page 25. – N. Shales May 04 '18 at 22:39
  • From N. Shales' link: "Remarkably, there are $3^{n-1}$ domino towers consisting of $n$ bricks. Equally remarkably, no simple bijection is known." – Peter Kagey May 04 '18 at 23:27
  • I think you need to be more explicit about what a "stable" configuration means. If, for example, we add a second brick to row 2 of your first figure and remove the middle brick in row 1, the 2 bricks in row 2 cannot move past each other. Is this a stable configuration? – Jens May 04 '18 at 23:31
  • @Jens, that's not stable, because the blocks are assumed to be frictionless—so any arbitrarily small downward force on the blocks above the hole would cause blocks to move. I'll add some clarification, thanks! – Peter Kagey May 04 '18 at 23:45
  • If they are frictionless, the tiniest lateral force to any brick would set that brick moving, along with any bricks in front of it. The tiniest torque to any "overhang" bricks would send the bricks above that brick moving. – Jens May 04 '18 at 23:57
  • To be pedantic, I mean "vertically stable", which is to say, arbitrarily small vertical forces. If I've done the free-body analysis correctly, a small vertical force to the cantilevered bricks in the second example wouldn't cause them to move. – Peter Kagey May 05 '18 at 00:01
  • 4
    This OEIS sequence and the paper it links to, seem relevant here. Balanced configurations (let alone stable ones) are trickier than one might think. E.g. I was surprised that diamond configurations are only balanced if the number of bricks in the largest row is $\lt 5$ (see page 3 in the paper). – Jens May 06 '18 at 00:25
  • Related : What exactly are the curves that are a best fit to the Harmonic Cantilever? – Han de Bruijn May 06 '18 at 10:49

1 Answers1

1

Although probably not a combinatorial rule per se, here is an algorithm that could be used to find unstable equilibria or configurations that would not be in equilibria:

1) Identify all bricks with only 1 supporting brick.

2) For each of these bricks consider the bricks above it connected to it by an upward facing V. (These are the only bricks that put any weight onto the brick, and therefore determine its stability.)

3) If this group of bricks has a center of gravity that is directly over the supporting brick, then the configuration is stable. If the center of gravity is directly over the edge of the supporting brick then it is unstable. If the center of gravity is over the unsupported side then it is not in equilibrium and will fall due to gravity.

4) If all singly supported bricks are in stable equilibrium, then the entire configuration is also. Else, if all singly supported bricks are either stable or unstable, then the configuration is unstable. Else, the configuration is not in an equilibrium.

Andrew
  • 349