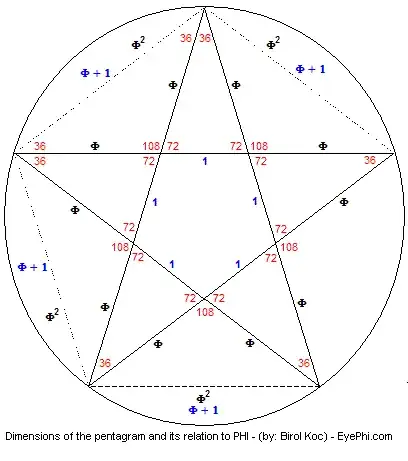
Please tell me if there is a duplicate; I can't find any question that does answer me; If you find one, I'll remove my question. Thank you :)
Prove that $2\cos36° = 2\sin18° +1$.
I saw people proving it by identities here, or I can also prove it by finding the exact value here and here, but what I'm trying to find is a way that (I hope) can be proven from this diagram, since both $\cos36°$ and $\sin18°$ have a close relationship with the golden ratio. Any help will be appreciated.
You can pull it off with your diagram, but you will also need $\color{blue}{\Phi^2=\Phi+1}$ (which is already implied in your diagram).
Take one of the isoceles triangles with sides $\Phi$, $\Phi$ and $1$; split it in half to obtain a right-angled triangle with sides $\Phi$, "something" and $1/2$; then you can compute $$\sin 18^\circ =\frac{1/2}{\Phi}$$ so that $$2\sin 18^\circ +1 =\frac{1}{\Phi} +1 =\frac{\color{blue}{1+\Phi}}{\Phi} =\frac{\color{blue}{\Phi^2}}{\Phi} =\Phi.$$
For $\cos 36^\circ$, take an isoceles triangle of sides $\Phi$, $\Phi$ and $\Phi^2$; split it in half to obtain a right-angled triangle with sides $\Phi$, "something" and $\Phi^2/2$; then you can compute $$\cos 36^\circ =\frac{\Phi^2/2}{\Phi} =\frac{\Phi}{2}.$$
Let the top vertex be called $A$, the left arm vertex be called $B$, the next line intersection on that very horizontal line be called $C$ the center point be called $D$, the next line intersection there be called $E$ and the right arm point be called $F$.
Then you already displayed that $AB=\Phi^2$. Thus from the triangle $ABD$ you get $$2\cos(36°)=2\frac{BD}{AB}=\frac{BF}{AB}=\frac{\Phi^3}{\Phi^2}=\Phi$$
On the other hand you have displayed that $AC=\Phi$. Thus $$2\sin(18°)=2\cos(72°)=2\frac{CD}{AC}=\frac{CE}{AC}=\frac1{\Phi}$$
And of course you know that $\Phi=1+1/\Phi$ or (multiplied by $\Phi$): $\Phi^2=\Phi+1$. In fact this can be also read off from the isoceles triangle $ABE$, because $AB=\Phi^2$ and $AB=BE=BC+CE=\Phi+1$.
--- rk
