0

Equation 7 of "Particle Shape Factors and Their Use in Image Analysis–Part 1: Theory" (PDF) defines circularity as

$$\text{circularity} = \sqrt{\frac{4\pi\cdot\text{area}}{\text{perimeter}^2}}$$

Which type of triangle has the largest circularity value, and how does one prove it?

Blue
  • 75,673
Abdulkader
  • 69

3 Answers3

2

enter image description here

In other words you want to find the triangle type that has the biggest ratio between area and perimeter squared.

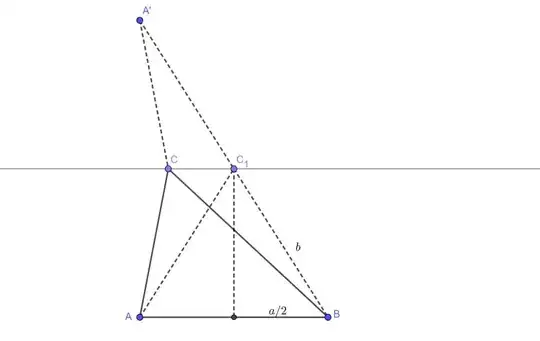
First, let us show that it has to be isosceles triangle. Suppose the opposite, that the triangle $ABC$ is optimal. Draw line through point $C$ parallel with $AB$ and find the mirror point $A'$ of $A$ with respect to that line. Line $BA'$ meets the parallel line at point $C_1$.

Obviously, triangles $ABC$ and $ABC_1$ have the same area but triangle $AMC_1$ has smaller perimeter because:

$$AC_1+BC_1=A'C_1+C_1B<BC+CA'=BC+AC$$

So triangle $ABC$ is not optimal and we should consider only triangles that are isosceles.

Supose that the perimeter $P=2s$ is fixed, base of the thriangle is equal to $a$ and leg to $b$. Let us maximize the area.

$$b=s-\frac a2$$

$$h=\sqrt{b^2-\frac{a^2}{4}}$$

$$h=\sqrt{(s-\frac a2)^2-\frac{a^2}{4}}$$

$$h=\sqrt{s^2-as}$$

$$A=\frac{ah}2=\frac12\sqrt{a^2s^2-a^3s}$$

So the area is maximized when the function

$$f(a)=a^2s^2-a^3s$$

...has maximm value. By solving equation:

$$f'(a)=0$$

...we get:

$$2as^2-3a^2s=0\implies a=\frac{2s}{3} \implies a=b=\frac P3$$

So the most "circular" triangle is actually an equilateral triangle.

Saša
  • 15,906
  • 2
    +1 for the diagram! But after proving that the triangle has to be isosceles (i.e. $AC$ has to be equal to $BC$), you are done, because an identical argument using $BC$ as the base shows that $AC$ has to be equal to $AB$. – TonyK Dec 21 '18 at 13:36
  • "Suppose the opposite, that the triangle ABC is optimal." -- you should first show the problem is compact before picking an optimal ABC. – user10354138 Dec 21 '18 at 14:24
  • @TonyK You are right, I have missed the most elegant solution: "Suppose that the optimal triangle ABC has a pair of sides of different lengths... Than comes the part with the diagram... And yes, we are done. Thanks! – Saša Dec 21 '18 at 14:54
  • @Oldboy Thank you – Abdulkader Dec 26 '18 at 10:38
2

Let's denote the circularity by $Z$. $$Z=(some\ constant)*\frac{(s(s-a)(s-b)(s-c))^{1/4}}{s},$$ since area$=(s(s-a)(s-b)(s-c))^{1/2}$ and perimeter$=2s$.

Note that $Z$ depends on $a,b$ and $c$. So, for $Z$ to be maximum, it's partial derivatives with respect to $a,b$ and $c$ will be $0$. It'll be a little long calculation, but at last, it'll give you three equations:- $$-\frac{s}{s-a}+\frac{s}{s-b}+\frac{s}{s-c}=3\ \ \ \ \ \ \ \ (1)$$ $$\frac{s}{s-a}-\frac{s}{s-b}+\frac{s}{s-c}=3\ \ \ \ \ \ \ \ (2)$$ $$\frac{s}{s-a}+\frac{s}{s-b}-\frac{s}{s-c}=3\ \ \ \ \ \ \ \ (3)$$ Add those to get $$\frac{s}{s-a}+\frac{s}{s-b}+\frac{s}{s-c}=9\ \ \ \ \ \ \ \ (4)$$ Now, by AM-HM inequality, $$\frac{(s-a)+(s-b)+(s-c)}{3}\geq \frac{3}{\frac{1}{s-a}+\frac{1}{s-b}+\frac{1}{s-c}}\ \ \ \ \ \ \ \ (5)$$ You can rearrange $(5)$ to get $(4)$. Note that equality holds iff all those terms are equal $\implies s-a=s-b=s-c\implies a=b=c$

Ankit Kumar
  • 1,874
1

Since the circularity measure of similar triangle is the same, we may normalize the triangles to have a fixed perimeter, say $1$, and then the problem is simply to find the triangle of maximum area and given perimeter.

It is well-known that the answer is an equilateral triangle. This is easy to show using Heron's formula and Lagrange multipliers, as is done here.

saulspatz
  • 53,131