Find for given supremum, epsilon.

Question

Need help in vetting my answers for Q. 1,2 in section 2.2.2 in chap. 2 (page 7) in CRM series book by MAA: Exploratory Examples for Real Analysis, By Joanne E. Snow, Kirk E. Weller. .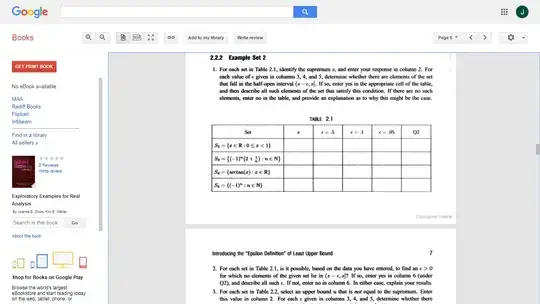

Q. 1:
For each set in Table 2.1, identify the supremum $s$ and enter your response in column 2. For each value of $\epsilon$ given in columns 3, 4, and 5, determine whether there are elements of the set that fall in the half-open interval $(s - \epsilon, s]$. If so, enter yes in the appropriate cell of the table, and then describe all such elements of the set that satisfy this condition. If there are no such elements, enter no in the table, & provide an explanation as to why this might be the case.

$$\begin{array}{c|c|c|c|c|} Set & \text{$s$} & \text{$\epsilon=.5$} & \text{$\epsilon=.1$} & \text{$\epsilon=.05$} & \text{$Q.\, 2$} \\ \hline \text 1)\,\ S_2 = \{x\in \mathbb{R}: 0\le x \lt 1 \} & 1 & yes & yes & yes &no\\ \hline \text 2)\,\ S_3 = \{(-1)^n(2+\frac 1n)\,: n\in \mathbb{N}\} & 2.5 & yes & yes & yes &no \\ \hline \text 3)\,\ S_4 = \{arctan(x)\,: x\in \mathbb{R}\} & \frac \pi{2} & yes & yes & yes &no\\ \hline \text 4)\,\ S_5 = \{(-1)^n\,: n\in \mathbb{N}\} & 1 & yes & yes & yes &no\\ \hline \end{array}$$

$S_2 = \{x\in \mathbb{R}: 0\le x \lt 1 \}:$
$s :$ The upper open bound is the supremum.
$\epsilon=.5 :(0.5, 1]$ : Yes, there are reals existing there.
$\epsilon=.1 :(0.9, 1]$ : Yes, there are reals existing there.
$\epsilon=.05 :(0.95, 1]$ : Yes, there are reals existing there.

$S_3 = \{(-1)^n(2+\frac 1n)\,: n\in \mathbb{N}\}$
$s :$ The function range alternates between positive & negative. The value $\frac 1n$ decreases with increasing $n$. So, the first positive value of $n=2$ yields the supremum $=2.5$.
$\epsilon=.5 :(2, 2.5]$ : Set $S_3 $ lies in reals with supremum in the set. No natural exists in this interval.
$\epsilon=.1 :(2.4, 2.5]$ : ----same as above ----
$\epsilon=.05 :(2.45, 2.5]$ : ----same as above ----

$S_4 = \{arctan(x)\,: x\in \mathbb{R}\}$
$s :$ $\frac{\pi}{2}$ is the supremum.
$\epsilon=.5 :(\frac{\pi}{2} - 0.5, \frac{\pi}{2}]$ : Yes, there are reals existing there.
$\epsilon=.1 :(\frac{\pi}{2} - 0.1, \frac{\pi}{2}]$ : Yes, there are reals existing there.
$\epsilon=.05 :(\frac{\pi}{2} - 0.05, \frac{\pi}{2}]$ : Yes, there are reals existing there.

$S_5 = \{(-1)^n\,: n\in \mathbb{N}\}$
$s :1$
$\epsilon=.5 :(0.5, 1] $ : Yes, there is single natural in $S_5$ existing there, i.e $=1$.
$\epsilon=.1 :(0.9, 1]$ : ----same as above ----
$\epsilon=.05 :(0.95, 1]$ : ----same as above ----

Q. 2. For each set in Table 2.1, is it possible, based on the data you have entered, to find an $\epsilon\gt 0$ for which no elements of the given set lie in $(s - \epsilon, s]$? If so, enter yes in column 6 (under $Q.\, 2$) and describe all such $\epsilon$. If not, enter 'no' in column 6. In either case, explain your results.

The answers here are based on fact that $\epsilon$ is concerned with range, hence its domain is defined by range.

> $S_2 = \{x\in \mathbb{R}: 0\le x \lt 1 \}:$
No, as only possible for $\epsilon=0$, or for 'the' real number just larger than $0$; which is not possible to find given the infinitude of reals between any two values.

Edit :
No, as only possible for $\epsilon=0$, as then the desired interval is : $(1,1]$; i.e. the point $=1$. But, this value of $\epsilon=0$ is not permitted.

> $S_3 = \{(-1)^n(2+\frac 1n)\,: n\in \mathbb{N}\}$
Yes, for $\epsilon=2.5$.

Edit :
$$\begin{array}{c|c|} & \text{$n\in \mathbb{N}$}& \text{$\{(-1)^n(2+\frac 1n)\}$}\\ \hline a & 1& -3 \\ \hline b & 2& 2.5\\ \hline c & 3& -\frac73=-2.\overline{33}\\ \hline d & 4& \frac94= 2.25\\ \hline d & 5& -\frac{11}5=-2.2\\ \hline d & 6& \frac{13}{6}=2.1\overline{6}\\ \hline d & 7& -\frac{15}{7}=-2.\overline{2.142857}\\ \hline d & 8& \frac{17}{8}=2.125 \\ \hline d & 9& -\frac{19}{9}=-2.\overline{1}\\ \hline \cdots \end{array}$$

$S_3=\{-3,-2.\overline{33},-2.2, -2.\overline{2.142857}, -2.\overline{1},\cdots,2.25,2.1\overline{6},2.125,2.5\}$ leading to no single value of $\epsilon\gt 0$ that enables no values of the set in given range of $(2.5-\epsilon, 2.5]$.

Say, take $\epsilon=0.1$. The desired range of values in which no value of set $S_3$ should fall is : $(2.5-0.1, 2.5]= (2.4, 2.5]$.
But, this is false, as at least one value of $s$ lies in this closed interval.

If the interval $(s - \epsilon, s]$ is a valid one, then at least would be having $s$.

> $S_4 = \{arctan(x)\,: x\in \mathbb{R}\}$
Yes, for $\epsilon=\frac{\pi}{2}$.

Edit :
$S_4=(-\frac{\pi}{2}, \frac{\pi}{2})$ leading to no single value of $\epsilon$ that enables no values of the set to lie in given interval $(\frac{\pi}{2}-\epsilon , \frac{\pi}{2}]$.

> $S_5 = \{(-1)^n\,: n\in \mathbb{N}\}$
No, as then need only one value of $\epsilon=0$.

Edit :
$S_5 = \{-1,1\}$ & the interval is $(1 - \epsilon, 1]$. This leads to any value of $0\lt \epsilon\lt 1$ to not satisfy the requirement that no value of the set to lie in the interval. A value of $0\lt \epsilon\ge 1$ will also not satisfy the requirement, as the lower bound is negative, leading to possibly both points in the set to lie in the interval.

Answer 1

If you find your $s$ correctly. Columns $3$ to $5$ must be yes and the last column must be no from definition of supremum.

For $S_3$, the supremum is $2.5 \in S_3$. Hence $s \in (s-\epsilon, s]$. Notice that the elements of the sets need not be natural number.

For $S_4$, if you pick $\epsilon = \frac{\pi}2$. We have $\arctan(1)=\frac{\pi}4 \in S_4$. Hence you didn't fill in the last column correctly.

Note that $\color{red}{S_5=\{-1,1\}}$. The supremum is $1$.

Response to your edit:

• For $S_i$, rather than there are real numbers in the interval, the real interest is there are elements of $S_i$ in the interval.

• For $S_5$, the supremum is $1$, not $\infty$. $S_5=\{1,-1\}$. The statement there are natural number existing there makes no sense.

• Also, domain and range are usually terminology associated with function.

• Question $2$ shouldn't be addressed individually:

What you need to argue for question $2$ is suppose on the contrary that such $\epsilon >0$ exists such that $(s-\epsilon, s] \cap S_i = \emptyset$, show that $s-\epsilon$ is an upperbound of $S_i$ as well which leads to a contradiction that $s$ is the least upper bound.