$ \sin 30° \sin x \sin 10° = \sin 20° \sin ({80°-x}) \sin 40° $
I tried transformation formulas , $ 2\sin a \sin b $ one. I know the value of sin 30° but what about others?
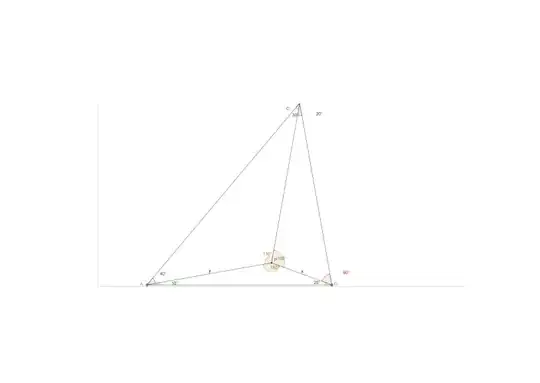
Original problem
In triangle ABC, P is an interior point such that $ \angle PAB = 10°. \angle PBA = 20° PAC = 40° \angle PCA = 30° $ then what kind of triangle it is ? I solved it till I got stuck here.
Assume AB = 1.
Apply sine law to PAB to get $PB = 2 \sin 10^0$.
Apply sine law to PAC to get $PB = 2 \sin 20^0$ and $PC = 4 \sin 20^0 \sin 40^0$.
Apply cosine law to PBC to get $BC$ in terms of those angles. Note that $\cos 100^0 = - \sin 10^0$.
$BC^2 = 4 \sin^2 10 + 16 \sin^220^0\sin^2 40^0 + 16 \sin 20^0 \sin 40^0 \sin^210^0$
Suggestion:- Convert all angles in $BC^2$to $\sin 10^0$ (or $\sin 20^0$) by compound angle formula. Hope that the result is 1.
Like Solve $\frac{\sin(xº)\sin(80º)}{\sin(170º - xº) \sin(70º)} = \frac {\sin(60º)}{\sin (100º)}$
$$\dfrac{\sin(80-x)}{\sin x}=\dfrac{\sin30\sin10}{\sin20\sin40}$$
$$\implies\sin80\cot x-\cos80=\dfrac{\sin30\sin10}{\sin20\sin40}=\dfrac{4\sin10\sin80}{2\sin(3\cdot20)}$$
using https://brainly.in/question/3475250
$$\implies\cos10\cot x=\sin10\left(1+4\cos10\tan30\right)$$
$$\implies\sqrt3\cot x=\sqrt3\tan10+4\sin10$$
Like Simplifying $\tan100^{\circ}+4\sin100^{\circ}$
set $A=360 n-3x$ in $2\sec A\sin x+\tan x=-\tan A$
$$2\sec3x\sin x+\tan x=\tan3x$$
Here $x=10\implies2\cdot\dfrac2{\sqrt3}\sin10+\tan10=\dfrac1{\sqrt3}\iff4\sin10+\sqrt3\tan10=1$
Can you take it from here?
