5

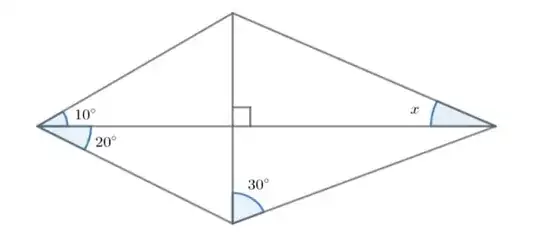
Solve: $$\frac{\sin(xº)\sin(80º)}{\sin(170º - xº) \sin(70º)} = \frac {\sin(60º)}{\sin (100º)}$$

I was solving a geometry problem with trigonometry, and after applying a lot of law of sines i got to this equation in 1 variable, but i'm not capable of solving it. The answer to the problem is $40º$, and by Wolfram Alpha i saw that this equation it's correct, but i don't know how to solve it by hand.

Any hints?

($xº$ is a value for an right triangle, that's why i'm looking for one solution.)

Here is the problem if anyone find a different answer:

enter image description here

Trobeli
  • 3,242

2 Answers2

3

$$\sin170=\sin10$$

$$\sin100=\sin80=\cos10$$

$$\cot(90-x)=\tan x$$

$$\tan10\cot x=\dfrac{\cos(70-60)}{\sin60\sin70}-1$$

$$=\cot70\cot60$$

$$\cot x=\tan20\tan80\cot60$$

Use Proving a fact: $\tan(6^{\circ}) \tan(42^{\circ})= \tan(12^{\circ})\tan(24^{\circ})$, to find

$$\tan20\tan40\tan80=\tan(3\cdot20)=?$$

Consequently $$\cot x=\cot40$$

lab bhattacharjee
  • 274,582
2

We can write your equation in the form $$\frac{\sin(100^{\circ})\sin(80^{\circ})}{\sin(60^{\circ})\sin(70^{\circ})}=\frac{\sin(170^{\circ}-x)}{\sin(x)}$$ And now we use the addition formulas $$\sin(170^{\circ}-x)=\sin(170^{\circ})\cos(x)-\cos(170^{\circ})\sin(x)$$ Dividing by $\sin(x)$ $$\sin(170^{\circ})\cot(x)-\cos(170^{\circ})$$ Now you can solve for $\cot(x)$

Dr. Sonnhard Graubner
  • 95,283