1

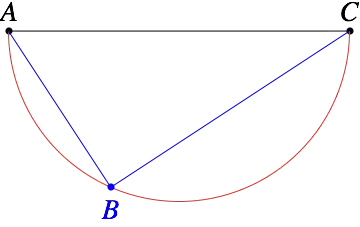
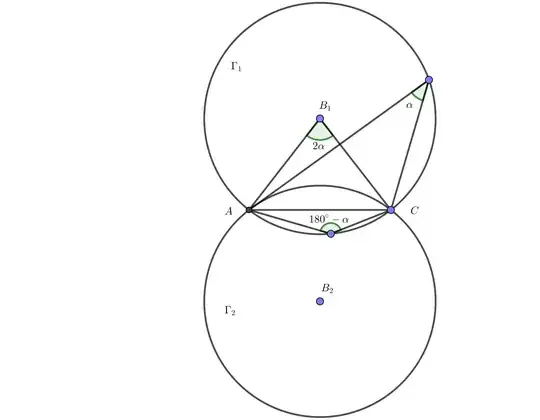
Consider two points $A$ and $C$ separated by a distance $d$. One can show through simple geometry that from any point $B$ on the semicircle having radius $d/2$ with $A$ and $C$ as specifying its diameter the angle $\angle ABC = 90^\circ$.

What is the name (and functional form) of the equivalent curve when the angle is some arbitrary fixed angle $0 \leq \angle ABC \leq 180^\circ$?

semicircle

David G. Stork
  • 29,774

2 Answers2

2

Hint. Build an isosceles triangle $ABC$ with basis $AC$ so that $\hat{B}$ has a pre-defined angle and consider the circle with center on $B$ and radius $BA$.

Full answer. Let $\alpha \in (0^\circ, 90^\circ)$ be a fixed angle. There are precisely $2$ isosceles triangles $AB_iC$ with basis $AC$ such that $A\widehat{B}_iC = 2 \alpha$. Since $2\alpha < 180^\circ$, it is possible to build these triangles. Also, notice that one is the reflection of the other by line $AC$. Let us denote by $\Gamma_i$ the circle centered on $B_i$ that has radius $AB_i$. Notice that the chord $AC$ breaks each circle $\Gamma_i$ into two arcs. Using the inscribed angle theorem, we know that in one of the arcs of $\Gamma_i$ the angle that any point sees arc $AC$ is precisely $\alpha$. On the complementary arc of $\Gamma_i$, the angle that any point sees $AC$ is $180^\circ - \alpha$, since for any inscribed quadrilateral the sum of opposing angles is $180^\circ$.

enter image description here

Community
  • 1
D. Ungaretti
  • 2,668
  • Well, certainly points on the circle you defined cannot satisfy the angle criterion. After all, the point $B$ (or $\hat{B}$) which satisfies the requirement (by construction) does not lie on that circle, since it is in the circle's center. – David G. Stork Sep 03 '19 at 00:13
  • But what about inscribed angles in this circle? Maybe I should have said to begin with an angle $\hat{B}$ with measure the double of the desired pre-determined angle. – D. Ungaretti Sep 03 '19 at 00:17
  • Please update your "answer" accordingly. (I still don't think your idea works.... but will continue to explore.) – David G. Stork Sep 03 '19 at 00:22
  • +1. But please change the names of the points to match those in the figure, or draw a better figure with GeoGebra. – Intelligenti pauca Sep 03 '19 at 08:53
  • @Aretino It was quite late yesterday... made my own figure with the construction now. – D. Ungaretti Sep 03 '19 at 18:15
  • @DavidG.Stork Is it understandable now? – D. Ungaretti Sep 03 '19 at 18:17
  • Yes... But your earlier approach either didn't include the crucial point $B$ (and how to locate it), so at that time I accepted @automaticallyGenerated's correct solution. Thanks for your help (+1). – David G. Stork Sep 03 '19 at 20:05
0

WLOG, assume that $A$ is at $(0, 0)$ and $C$ is at $(d, 0)$. We then need to find all points $B = (x, y)$ such that $\angle ABC = \theta$.

We have that $$\tan(\theta) = \frac{-yd}{x(x-d)+y^2}$$

For now, let's assume that $y > 0$. The other half of the answer will just be the reflection over the $x$-axis. We then have that $$x^2\tan(\theta)-dx\tan(\theta)+y^2\tan(\theta)+yd=0$$

As you can see, each half is part of a circle with radius $d\csc(\theta)/2$ centered at $(d/2, \pm d\cot(\theta)/2)$ going to the $x$-axis.

Varun Vejalla
  • 8,873