I can't solve the following problem:
Prove that triangle $ABC$ with known side $AC$ and angle $B$ has maximum perimeter when $AB=BC$.
Purely geometric proof is preferred, calculus is not allowed.
I started by assuming the triangle is circumscribed by a circle uniquely determined by $AC$ and $\angle B$, and showing that triangle height perpendicular to $AC$ is maximized when it divides $AC$ in half. Which means that area is maximized when $AB=BC$. Which leads to $AB\times BC \gt AM\times MC$, where M is some other point on the circle. And there I'm stuck, not sure how to continue further.
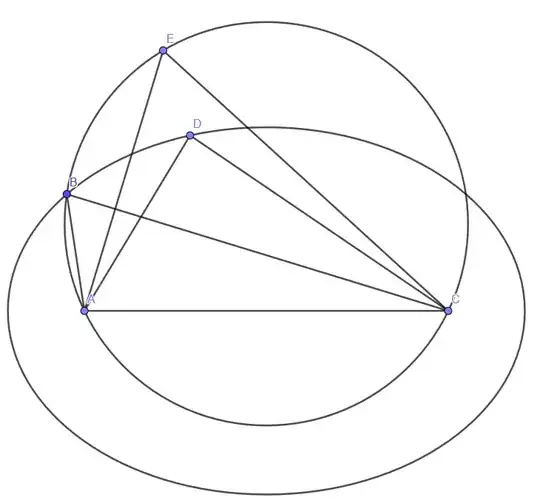
Basically, If triangle ABC is inscribed in a circle, then the measure of angle A is one-half the measure of arc BC.
– Steven Alexis Gregory Jul 20 '21 at 20:56