Inverted Triangle Burgers' Equation

Question

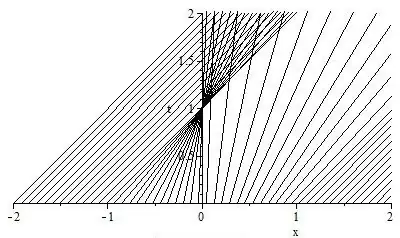
I wish to solve the so-called Burgers' equation $u_t+uu_x=0$ with the initial data $$u(x,0)=\begin{cases} 1 & x<-1\\ -x & -1\leq x\leq 0\\ x & 0\leq x\leq 1\\ 1 & x>1 \end{cases}$$

I'm having trouble drawing the characteristic lines, but I know that the slope of the initial data (wrt t) corresponds to the value of the solution. Furthermore, I also see that there should be a shock formation at $t=-1$ (I think?)

Thank help is appreciated

Answer 1

Similarly to this post, the breaking time where a shock wave forms is $$ t_b= \frac{-1}{\inf u_x(x,0)} = 1 \, . $$ The base characteristics represented below in the $x$-$t$ plane illustrate this feature: