2

There is a problem here in Q. $5$ on the last page. It states to find coordinates of point $p$.

Image

Taking point $a=(3,2,5,1), \ b=(3,4,7,1), \ c= (5,8,9,3)$.
Also, $b$ has two coordinates in common with $a$, and $p$ lies on the same line as $a,b$.
So, those two coordinates of $p$ are same as $a,b$. Hence, $p= (3,x,y,1)$; where $x,y\in \mathbb{R}$ are unknown.

Given that $\triangle acp, \triangle bcp$ are right-angled; get:

$1. \ \ \triangle acp:\ \ \ \ \ {ac}^2 = {ap}^2 + {cp}^2\implies({(-2)}^2+6^2+4^2+2^2) = ({(x-2)}^2 +{(y-5)}^2) + (2^2+{(8-x)}^2+{(9-y)}^2+{(-2)}^2 )$
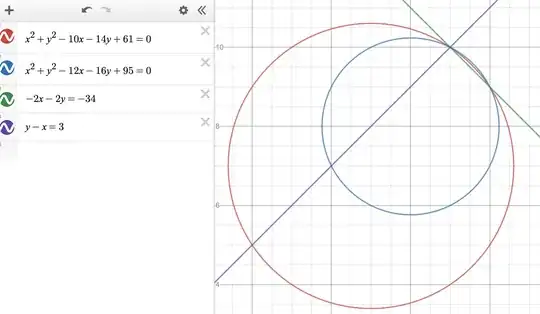
$60 = 2x^2+2y^2-20x-28y+182\implies x^2+y^2-10x-14y+61=0$

$2. \ \ \triangle bcp:\ \ \ \ \ {bc}^2 = {bp}^2 + {cp}^2\implies(2^2+4^2+2^2+2^2) = ({(x-2)}^2 +{(y-5)}^2) + (2^2+{(8-x)}^2+{(9-y)}^2+{(-2)}^2 )$
$28 = 2x^2+2y^2-20x-28y+190\implies x^2+y^2-12x-16y+95=0$

From $1,2$, get: $-2x -2y +34 = 0\implies x +y -17=0$.

But, how to proceed it further to find coordinates of $p$ is unclear.

jiten
  • 4,524
  • 1
    Mor precisely, $p=a+t(b-a)=(3,2t,2t,1)$ is the line equation with directing vector $b-a$ passing through $a$ and you get $1$ equation with $1$ variable then. Should I make it an answer? – Alexey Burdin Jun 29 '20 at 16:48
  • @AlexeyBurdin Please elaborate with answer. Thanks a lot. – jiten Jun 29 '20 at 16:49

2 Answers2

1

Having $p=(3,x,y,1)$ does not reflect that $p$ is on the line $ab$. However, parametric equation of an arbitrary line passing through arbitrary points $a,\,b$ in Euclidean space is $x=a+t(b-a)$ with some parameter $t\in \mathbb{R}$, hence $$p=a+t(b-a)=(3,2,5,1)+t\,(0,2,2,0)$$ or, more compactly $$p=(3,2+2t,5+2t,1)$$ and your further computations will succeed as we have only one equation $$(b-a)\cdot(p-c)=0\;(\Leftrightarrow (b-a)\perp (p-c))$$ in other words, the two equations in the OP solution are equivalent and do not give solutions to two variables. $$(0,2,2,0)\cdot((3,2+2t,5+2t,1)-(5,8,9,3))=0$$ $$(0,2,2,0)\cdot(-2,2t-6,2t-4,-2)=0$$ $$2\cdot(2t-6)+2\cdot(2t-4)=0$$ $$t=\frac{5}{2}$$ $$p=(3,7,10,1)$$ Verification, for a case of a typo: $(b-a)\cdot(p-c)=0$.

Alexey Burdin
  • 5,214
  • But am not clear why my approach failed. – jiten Jun 29 '20 at 17:27
  • Because the restiction $p=(3,x,y,1)$ is more broad (it's a 2d-plane in 4d) than $p=(3,2+2t,5+2t,1)$ which is clearly a line. Let me know if it does not make much sense. Thanks. – Alexey Burdin Jun 29 '20 at 17:48
  • Sorry for delay. I meant that in OP took two quadratic eqns. to derive $x+y=17$, but could not pursue further. Is there any additional step that can be used in my approach. – jiten Jun 29 '20 at 19:32
  • 1
    I think no. That is just a co-incidence that 1st and 4th coordinates of $a,b$ were the same. What do you do if there are one same coordinate only or all different? In your approach as the equations are correct, plugging $y=17-x$ back into one of the equations gives $(x,y)=(7,10)$ or $(8,9)$. However, $(3,8,9,1)$ is not on the line $ab$. – Alexey Burdin Jun 29 '20 at 20:11
  • Have a similar problem: find $y$- intercept of the line between $r_1=(1+i)$ and $r_0=(0,-1)$. Unable to use your approach. Could only lead to $(0,-1)(1-t)+ t.(1,i)$ I am taking $0\le t \le 1$, as taking the vector only on limited interval between $r_0, r_1$. Please help pursue. – jiten Jul 09 '20 at 02:21
  • 1
    Can't see what are points on the line. Is $i$ the $(1,0)$ vector of $\sqrt{-1}$?. When you consider a line, $t$ is unlimited. If $t$ is limited, $ta+(1-t)b$ yields to the segment between the points $a$ and $b$. Can you please link your question here? I'll see. Not sure how exactly the intercepts work in complex coordinates, maybe another way, try to see $i$ as a vector (actually, $1$ and $i$ form a basis) then? Anyway, more details needed. Thanks. – Alexey Burdin Jul 09 '20 at 02:39
  • Sorry, my last comment was wrong as $r_0 =(-1,0)$. The two points are stated as $1+i, -1$; which should mean as $r_0 =(-1,0), r_1=(1,1)$. – jiten Jul 09 '20 at 02:48
  • 1
    You can do it yourself) $t(-1,0)+(1-t)(1,1)=(0,y)$, $(-t+1-t,0+1-t)=(0,y)$, $1-2t=0$, $t=\frac 12$, looking back wasn't it obvious? That $\frac12 (-1,0)+\frac 12(1,1)=\left(0,\frac 12\right)$?) Thanks, was pleasure solving this. – Alexey Burdin Jul 09 '20 at 02:55
  • Another way is to take scalar product of vectors perpendicular. Denote $y$- intercept as $r_c$ by C, $r_0$ by A, $r_1$ by B, origin as O. Take dot product of two lines: OA, OC.

    Can take the $y$ intercept as $r_c= r_0(1-t) + t.r_1, 0\le t \le 1$. (am limiting the vector to be from $r_0 $ to $r_1$ only, so limits on $t$, rather than $t\in \mathbb{R}$.

    Para. coord. of vector OA = $(1,0)$, & of vector OC = $(-1+2t, t)$. The dot product should be $=0$, so OA.OC $=0 \implies (1,0).(-1+2t, t)= 0 \implies -1+2t = 0 \implies t = 0.5$. Hence intercept has coord.: $(-1+1, 0.5)= (0, 0.5)$.

     – jiten Jul 09 '20 at 03:54
  • 1
    Please see here. Thanks. – Alexey Burdin Jul 10 '20 at 06:23
  • My last comment (very sorry that it was deleted by accident) was for problem no. 4 at: https://i.stack.imgur.com/JJZvQ.png. It was also made a post with identical contents at: https://math.stackexchange.com/q/3751706/424260. – jiten Jul 10 '20 at 12:12
1

Using the property of inner product directly is neater.

You can still use the information that $a, b, p$ is collinear.

$$\frac{x-2}{4-2}=\frac{y-5}{7-5}$$

$$x-2=y-5$$

$$y-x=3$$

Along with what you found $$x+y=17$$

We have $y=10$, $x=7$.

Hence $p=(3,7,10,1).$

enter image description here

Remark: the picture also illustrated that the two circles intersects at two points, hence you still have to rule out one of them say by using collinearity.

Siong Thye Goh
  • 149,520
  • 20
  • 88
  • 149
  • Please elaborate your 'Remark', as the other answer gives a link using wolfram, that uses only one equation. However, it still is able to filter out $(x,y)=(8,9)$ as a root, albeit by checking values of $t$ obtained by the two equations: $2t =6, 2t =7$. – jiten Jul 02 '20 at 09:39
  • 1
    inner product is the right way to go, the problem stays linear, you would not end up with two solutions. I just play along your working of using distances and we are dealing wiht quadratic equations. – Siong Thye Goh Jul 02 '20 at 10:26
  • Please see my post concerning- derivation of formula for cross-product, at : https://math.stackexchange.com/q/3742326/424260 – jiten Jul 02 '20 at 10:28