The problem is taken from here.
It's given $ABCD$ an isosceles trapeziois with $A:=(2,6,-3,9)$, $B:=(4,4,7,3)$, $C:=(8,2,7,-1)$, $AB||CD$, $\angle C=\angle D=60^\circ$, find $D$.
I want to present at least $3$ different solutions, so the post may appear rather lengthy.
The common part:
Let's make sure $\angle B=120^\circ$:
$$\cos\angle B=\frac{
\overrightarrow{BA}\cdot \overrightarrow{BC}
}{
|\overrightarrow{BA}|\cdot |\overrightarrow{BC}|
}=-\frac12$$
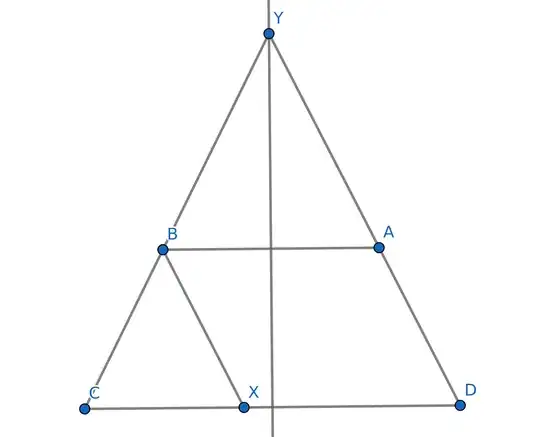
Let $X\in CD$, $|CX|=|CB|$ then $\triangle CBX$ is equilateral, $BADX$ is a parallelogram, thus $$\overrightarrow{CD}= \frac{|\overrightarrow{BC}|}{|\overrightarrow{BA}|} \overrightarrow{BA}+\overrightarrow{BA}$$ $$D=\left(\frac{|B-C|}{|B-A|}+1\right)(B-A)+C=(5, 5, -8, 8)$$
Let line $CB$: $Y=yB+(1-y)C$ and $Y$ be the intersection of the line $CB$ with perpendicular bisector hyperplane of $AB$: $(Y-\frac{B+A}{2})\cdot \overrightarrow{BA}=0$. Combining this together we find $y$ and thus $Y$: $$\left(yB+(1-y)C-\frac{B+A}{2}\right)\cdot(A-B)=0$$ $$y(B-C)\cdot(A-B)=-\left(C-\frac{B+A}{2}\right)\cdot(A-B)$$ $$y=-\frac{\left(C-\frac{B+A}{2}\right)\cdot(A-B)}{(B-C)\cdot(A-B)}$$ $$y=3\hbox{ and }Y=(-4, 8, 7, 11)$$ Because $\triangle YCD$ is equilateral, $YC=YD$ and $$\overrightarrow{YD}= \frac{|\overrightarrow{YC}|}{|\overrightarrow{YA}|}\overrightarrow{YA}$$ $$D=\frac{|\overrightarrow{YC}|}{|\overrightarrow{YA}|}\overrightarrow{YA}+Y= (5, 5, -8, 8)$$
Now let $D$ ob the line, parallel to $AB$, passing through $C$: $D=C+t(A-B)$. Let's use $\angle ADC=60^\circ$ directly: $$\cos \angle ADC= \frac{ \overrightarrow{DA}\cdot\overrightarrow{DC} }{ |\overrightarrow{DA}|\cdot|\overrightarrow{DC}| }= \frac{(C+t(A-B)-A)\cdot(t(A-B))}{ |C+t(A-B)-A|\cdot|t(A-B)| }=\\ \frac{(C+t(A-B)-A)\cdot(A-B)}{ |C+t(A-B)-A|\cdot|(A-B)| }=\frac{1}{2}$$ Performing multiplications and lengths as square roots of squares of corresponding vectors, we get $$\frac{36\cdot(-5 + 4t)}{6\sqrt{7 - 10t + 4t^2}\cdot 12}=\frac{1}{2},$$ squaring, rearranging and solving for $t$ we get $$3 - 5t + 2t^2=0$$ $$t=\frac{3}{2}$$ (the other root corresponds to $-5 + 4t\lt 0$). Thus $$D=C+t(A-B)=(5, 5, -8, 8)$$ Not tired yet?) The fourth solution:
Again let $D=C+t(A-B)$ and the perpendicular bisector of $AB$ be $\mathbf{n}\cdot\left(\mathbf{x}-\frac{A+B}{2}\right)=0$ where $\mathbf{n}=B-A$. Then, for symmetry relative to the perpendicular bisector, we get $$\mathbf{n}\cdot\left(A-\frac{A+B}{2}\right)=- \mathbf{n}\cdot\left(B-\frac{A+B}{2}\right),\\ \mathbf{n}\cdot\left(C-\frac{A+B}{2}\right)=- \mathbf{n}\cdot\left(D-\frac{A+B}{2}\right)$$ plugging $D$ into the latter equation we get a linear with respect to $t$, solving we get $t=\frac{3}{2}$ again.
All the numbers conputations are here.
@jiten's solution from the comment (https://math.stackexchange.com/questions/3739053/find-coordinates-of-point-in-mathbbr4/3739095#comment7716150_3739095) (I didn't quite get it):
Q.4 image, need coord. point $p$ in trapezoid with: A$(2,6,-3,9)$, B$(4,4,7,3)$, C$(8,2,7,-1)$, p$(x, y, z, w)$.
DV line BA$<-2, 2, -10, 6>$.
Param. form point on line $r(t)= (4,4,7,3) + t(-2, 2, -10, 6) = (4-2t, 4+2t, 7-10t, 3 +6t), t\in \mathbb{R}$.
Also, for line pC $r_1(t) = (8,2,7,-1) + s(-2, 2, -10, 6) = (8-2s, 2+2s, 7-10s, 3 +6s), s\in \mathbb{R}$;
with $s=1$ for vertex p $(8-2s, 2+2s, 7-10s, 3 +6s)\implies (6, 4, -3, 9)$.
Need verify by addl eqns. Say, find intersection lines Ap, Cp; with DV line Cp $= <x-8, y-2, z-7, w +1>$, of line Ap $=<x-2, y-6, z+3, w-9>$. But, not working.