Nice inequality with exponents $a^{2b}+b^{2a}\leq a^{\Big(\frac{a(1-a)(\frac{1}{2}-a)}{4}\Big)^2}$

Question

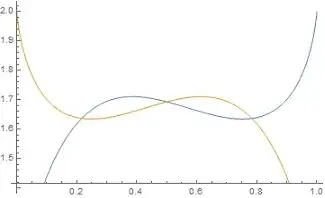
Hi it's a little refinement to play with a hard inequality of Vasile Cirtoaje :

Let $a\geq b>0$ such that $a+b=1$ then we have : $$a^{2b}+b^{2a}\leq a^{\Big(\frac{a(1-a)(\frac{1}{2}-a)}{4}\Big)^2}=f(a)$$

It implies directly the inequality of Vasile Cirtoaje .

I have tried the substitution $a=\sinh^2(x)$

$$\sinh(x)^{4\cosh^2(x)}+\cosh(x)^{4\sinh^2(x)}\leq \sinh(x)^{\Big(\frac{\cosh^2(x)\sinh^2(x)(\frac{1}{2}-\sinh^2(x))}{2}\Big)^2}$$

But I think it's nothing .

If we take one element of the sum and make the difference with the RHS and finally use derivatives it becomes awful . So I think it's a wrong way .

I have tried obviously Bernoulli's inequality as :

$$a^{2(1-a)}\leq 1+(a^2-1)((1-a)) \quad, (1-a)^{2(a)}\leq 1+((1-a)^2-1)(a)$$

But I don't know what to do next maybe there exists a reversed Bernoulli's inequality (?).Now I'm stuck because it's a hard nut (it could be my song).

Thanks in advance for all your advices and others things!

Little update

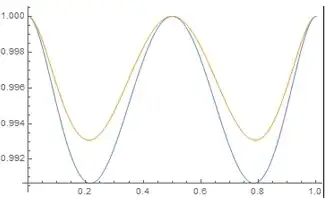
Maybe we can compare the upper bound got with Bernoulli's inequality with an inequality of the kind : $$1+\Big(\frac{a(1-a)(\frac{1}{2}-a)}{4}\Big )^{\alpha}\leq a^{\Big(\frac{a(1-a)(\frac{1}{2}-a)}{4}\Big)^2}=f(a)$$

We can determine easily $\alpha$ numericaly .

Answer 1

The inequality for $0\le b\le 1/2$, $a+b=1$, $$a^{2b}+b^{2a}\leq a^{\Big(\frac{ab(b-a)}{8}\Big)^2}\tag{1}$$ can be strengthened to $$a^{2b}+b^{2a}\le e^{-3a^2b^2(b-a)^2/4}\tag{2}$$ noting that $e^{-3a^2b^2(b-a)^2/4}\le a^{\Big(\frac{ab(b-a)}{8}\Big)^2}$ unless $a$ is almost $0$.

Only a sketch proof is given here, for what it's worth.

For brevity, let $f(x):=x^{1-x}$ and $g(x):=x^2(1-x)^2(x-\frac{1}{2})^2$. The claim is $$f(x)^2+f(1-x)^2\le e^{-3g(x)}$$

Trivially, $f(x)\ge x$, $f(0)=0$, $f'(0)=1$, $f(1)=1$, $f'(1)=0$. $f'(x)=\frac{1-x-x\ln x}{x^x}$.

Proposition 1. $f'(x)=0\iff x=1$

Proof: $\frac{1}{x}-\ln x=1$, equivalent to $\frac{1}{x}+\ln\frac{1}{x}=1$, so $x=\frac{1}{W(e)}=1$. ($W$ is Lambert's function.)

Proposition 2. $f(x)^2+f(1-x)^2$ has three local maxima, at $x=0,\frac{1}{2},1$.

Proof: The maxima/minima of $f(x)^2+f(1-x)^2$ occur when $f(x)f'(x)=f(1-x)f'(1-x)$.

At $x=0$, $f(0)=0=f'(1)$; at $x=1$, $f(1-x)=0=f'(1)$. Otherwise, divide by $f(x)$, $f(1-x)$.

At $x=0$, $$f(x)^2+f(1-x)^2=e^{2(1-x)\ln x}+e^{2x\ln(1-x)}=x^2+o(x)+1-2x^2+o(x)=1-x^2+o(x)$$ Hence $x=0$ is a local maximum. By symmetry, so is $x=1$.

The function $\frac{f'(x)}{f(1-x)} = \frac{1-x-x \ln x}{(x(1-x))^x}$ lies between $1$ and $2$, and has one local maximum and one local minimum. A sketch is as follows (blue curve).

$\frac{f'(x)}{f(1-x)}=\frac{f'(1-x)}{f(x)}$ at three places; the intersections are simple. Since $x=0$ is a local maximum, it follows that the only other local maximum is at $x=1/2$. Then $f(1/2)=1$.

Corollary $F(x):=-\ln(f(x)^2+f(1-x)^2)$ also has three local minima at $x=0,\frac{1}{2},1$.

A Taylor expansion at each point gives $F(0+h)=h^2+o(h)$, $F(1/2+h)=ch^2+o(h)$ where $c=4 - 4\ln2 - 2\ln^22\approx0.267$, $F(1-h)=h^2+o(h)$.

Hence fitting a polynomial with double roots at $x=0,\frac{1}{2},1$, namely $\alpha g(x)$, a necessary condition for $\alpha g(x)\le F(x)$ is $\alpha\le \min(4,16c)=4$. A sketch of $F(x)$ shows that the worst cases are at these points; and that $\alpha\le3$ is sufficient for $F(x)\ge3g(x)$. No simple proof for this, just a splitting into ranges $[0,1/8]$, $[1/8,3/8]$, $[3/8,1/2]$, and use Taylor series on each.

Proposition 3. For $x>e^{-16\alpha}$, $$e^{-\alpha g(x)}\le x^{(g(x)/4)^2}$$

Proof: Follows from $-\alpha g(x)\le g(x)\ln x/16$, equivalent to $\ln x\ge-16\alpha$, or $x\ge e^{-16\alpha}$.