This is a late solution, after the structural solution of pisco was already accepted, it also uses the elliptic curves intuition, and tries to give a "simpler substitution" and the way to obtain it. The substitution is
$$X = \frac{x^3+4}{x^2}\ ,$$
but let us see how first it was obtained free of charge, since this is the main point. I will give full details of the computations, CAS support, and show the pictures of the involved elliptic curve paths.
(1) How to obtain the substitution?
(The reader considering sage code annoying may please completely skip (1) and extract only the information that an isogeny killing the $3$-torsion point $(0,1)$
is used.)
The given integral can be seen as the integral of the invariant differential $dx/y$ on the path $\gamma$
from the point $P=(x_0,y_0)=(0,1)$ to
$Q=(x_1,y_1)=(2,3)$ on $E(\Bbb R)$, where $E$ is the elliptic curve given by the (affine) equation:
$$
E\ :\ y^2=x^3+1\ .
$$
In a picture:
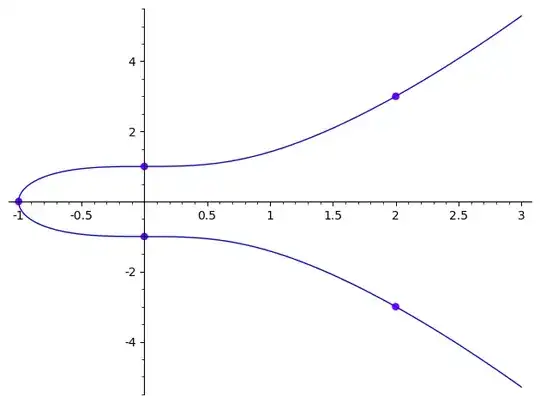
Just for the protocol: This was obtained in sage via:
sage: E = EllipticCurve(QQ, [0, 1])
sage: points = [E(P) for P in [ (-1,0), (0,1), (0,-1), (2,3), (2,-3) ]]
sage: pic = E.plot(xmin=-2, xmax=3)
sage: for P in points:
....: pic += point(P.xy(), size=40, rgbcolor=hue(0.75))
....:
sage: pic
As the OP remarks, there would be no problem to compute the integral from $P=(0,1)$ to the infinity point using the substitution $t=x^3+1$ to introduce the beta function, but we integrate from $P$ to $Q$, and the same substitution leads to an "incomplete beta" value. So the problem is the upper integration limit $2$ corresponding to $Q$.
We would like to use an algebraic substitution and move $Q$ to a "simpler point" (possibly on some other elliptic curve).
Note that the points that appear have finite order, using sage to print this information...
sage: for P in points:
....: print(f'The point {P.xy()} has order {P.order()}')
....:
The point (-1, 0) has order 2
The point (0, 1) has order 3
The point (0, -1) has order 3
The point (2, 3) has order 6
The point (2, -3) has order 6
The idea to proceed is natural, we use the isogeny which "simplifies" the complicated torsion point $Q=(2,3)$ of order $6$. Note that $2Q=P$ on $E$:
sage: P, Q = E.point((0,1)), E.point((2,3))
sage: 2*Q == P
True
(So using the isogeny which "kills" $P$ will also "simplify" $Q$.)
We ask sage for this isogeny in the one-liner:
sage: phi = E.isogeny(kernel=P)
and let it give us its underlying information:
sage: phi
Isogeny of degree 3
from Elliptic Curve defined by y^2 = x^3 + 1 over Rational Field
to Elliptic Curve defined by y^2 = x^3 - 27 over Rational Field
sage: phi.rational_maps()
((x^3 + 4)/x^2, (x^3*y - 8*y)/x^3)
sage: phi(P), phi(Q)
((0 : 1 : 0), (3 : 0 : 1))
This leads to a map $\phi:(x,y)\to\phi(x,y)=(X,Y)$ between the elliptic curves
$$
\begin{aligned}
E\ :\qquad && y^2 &= x^3+1\text{ and}\\
E'\ :\qquad && Y^2 &= X^3-27\text{ given by the passage}\\
&& X &=\frac{x^3+4}{x^2}\ ,\\
&& Y &=y\cdot\frac{x^3-8}{x^3}\ .
\end{aligned}
$$
and the image curve is $Y^2=X^3-27$, the path $\gamma$ from $P$ to $Q$ on $E(\Bbb R)$ becomes the path $\gamma'$ from $P'=\infty$ to $Q'=(3,0)$ on $E'(\Bbb R)$.
I can plot only $Q'$ on $E'(\Bbb R)$...
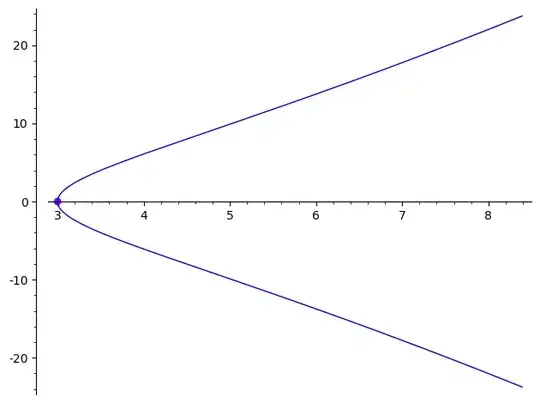
So we integrate alternatively the invariant differential form $dX/Y$ on the "upper branch" starting from $Q'=(3,0)$ to the infinity point.
Indeed, the above expressions $X,Y$ satisfy:
$$
\begin{aligned}
X^3-Y^2
&=\frac{(x^3+4)^3}{x^6}-\underbrace{y^2}_{x^3+1}\cdot\frac{(x^3-8)^2}{x^6}\\
&=\frac 1{x^6}
\Big[\
(x^9+12x^6+48x^3+64)
-
(x^9-15x^6+48x^3+64)
\ \Big]
\\
&=27\ .
\end{aligned}
$$
(2) Using the substitution:
We formally use $X=(x^3+4)/x^2$, $Y=y(x^3-8)/x^3$, and compute formally:
$$
\begin{aligned}
dX &= \left(x+\frac 4{x^2}\right)'\; dx
= \left(1-\frac 8{x^3}\right)\; dx
= \frac {x^3-8}{x^3}\; dx
\ ,\text{ so as expected}\\
\frac{dX}Y
%&=\frac {x^3-8}{x^3}\; dx\cdot\frac {x^3}{y(x^3-8)}\\
&=\frac{dx}y\ .
\end{aligned}
$$
(The isogeny connects the invariant differentials.)
This gives:
$$
\begin{aligned}
\int_0^2\frac {dx}{\sqrt{x^3+1}}
&=
\int_{\gamma\text{ from }(0,1)\text{ to }(2,3)\text{ on }E(\Bbb R)}
\frac{dx}y
\\
&=
\int_{\gamma'\text{ from }(3,0)\text{ to }\infty\text{ on }E'(\Bbb R)}
\frac{dX}Y
\\
&=
\int_{Y=0}^{Y=\infty}
\frac{d(Y^2+27)^{1/3}}Y
=\int_0^\infty \frac 23(Y^2+27)^{1/3-1}\; dY
\\
&\qquad\text{ (Substitution: $27t=Y^2+27$, $Y=27^{1/2}(t-1)^{1/2}$)}
\\
&=\int_1^\infty
\frac 23\cdot 27^{-2/3}\; t^{-2/3}\; 27^{1/2}\; \frac 12(t-1)^{-1/2}\; dt
\\
&\qquad\text{ (Substitution: $u=1/t$)}
\\
&=\int_0^1
\frac 13\cdot 3^{-2}\; u^{2/3}\; 3^{3/2}\; (1-u)^{-1/2}\; u^{1/2}\; \frac 1{u^2}\;du
\\
&= 3^{-3/2}\int_0^1 u^{1/6-1}\; (1-u)^{1/2-1}\;du
\\
&= 3^{-3/2}B\left(\frac 16,\frac 12\right)
\ .
\end{aligned}
$$
$\square$
(3) Note:
The above value involving the beta function $B$ is equal to
$\frac 16B\left(\frac 16,\frac 13\right)$, use for this the multiplication theorem for the gamma function:
$$
\Gamma\left(\frac 13\right)
\Gamma\left(\frac 23\right)
\Gamma\left(\frac 33\right)
=(2\pi)\;3^{-1/2}\;\Gamma(1)\ .$$

