6

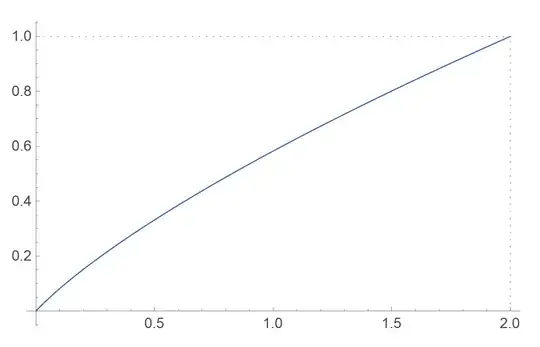
Consider a continuous real-valued monotone increasing function $f:\mathbb R^+\to\mathbb R^+$ satisfying $f\!\left(x+x^\phi\right)=x,$ where $\phi=\frac{1+\sqrt5}2$ is the golden ratio. Here is a plot of the function $f(z)$:

I need to find an asymptotic expansion of $f(z)$ for $z\to0^+$ in terms of powers of $z$. By manually balancing coefficients, I was able to find a few first terms: $$f(z)=z-z^\phi\color{red}+\phi\,z^{2\,\phi-1}+\mathcal O\left(z^{3\,\phi-2}\right), \quad z\to0^+.$$ How can I find more terms and, ideally, a general formula for all terms of this series?

Update: A wrong sign in formula is corrected (red).

Vladimir Reshetnikov
  • 47,122
  • 2
    See the comments here and here. $f(z)$ is a Fox-Wright function: $$f(z) = \sum_{j \geq 0} \frac {(-1)^j \hspace {1.5 px} \Gamma(1 + \phi j)} {\Gamma(2 + (\phi - 1) j)} \frac {z^{(\phi - 1) j + 1}} {j!}, \quad 0 < z < \phi^{-\phi \sqrt 5}.$$ – Maxim Jan 01 '21 at 06:44

1 Answers1

5

I notice that factoring $z$ out yields $f^{-1}(z)=z\big(1-z^{1/\varphi}\color{Red}{+}\varphi z^{2/\varphi}+\mathcal{O}(z^{3/\varphi})\big)$. Thus, let's write

$$ f^{-1}(z)=z\sum_{k=0}^{\infty} a_k z^{k/\varphi} $$

for some coefficients $a_k$ with $a_0=1$. Substitute $z=x+x^{\varphi}=x(1+x^{1/\varphi})$ to get

$$ x=x(1+x^{1/\varphi})\sum_{k=0}^{\infty} a_k(1+x^{1/\varphi})^{k/\varphi}x^{k/\varphi}. $$

Divide by $x(1+x^{1/\varphi})$, then expand Newton-Binomial series:

$$ \frac{1}{1+x^{1/\varphi}} = \sum_{k=0}^{\infty} a_kx^{k/\varphi}(1+x^{1/\varphi})^{k/\varphi} $$

$$ \begin{array}{ll} \displaystyle \sum_{n=0}^\infty (-1)^nx^{n/\varphi} & \displaystyle = \sum_{k=0}^{\infty} a_k x^{k/\varphi}\sum_{j=0}^{\infty} \binom{k/\varphi}{j}x^{j/\varphi} \\ & \displaystyle =\sum_{n=0}^\infty x^{n/\varphi} \left[\sum_{k=0}^n \binom{k/\varphi}{n-k} a_k\right]. \end{array} $$

Equating coefficients yields a recurrence for $a_n$:

$$ a_n=(-1)^n-\sum_{k=1}^{n-1} \binom{k/\varphi}{n-k}a_k. $$

This also shows there's a sign error in your quadratic term.

anon
  • 151,657