2

I have tried this question as follows:

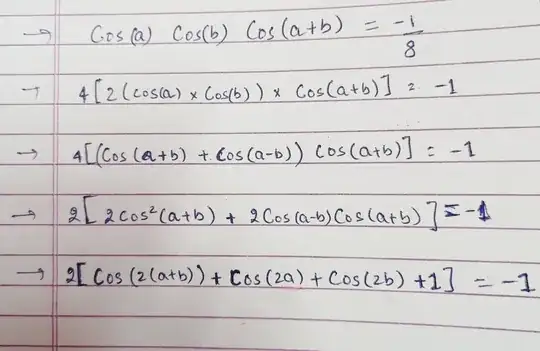
$$4[2(\cos(a)\cos(b))\cos(a+b)] = -1$$ My work!!

Then converted the $2\cos(a)cos(b)$ in $\cos(a+b) + \cos(a-b)$.

And so on but this got messy and big.

Another approach that I tried was that as $a$ and $b$ lie in the first quadrant then their cosine is positive this implies $\cos(a+b)$ is negative.

And without losing generality we can say each term be equal to 1/2 which implies

$a = b = π/3$.

I googled it but didn't find any solution.

Wolfram alpha after converting into the same thing as I have converted used complex numbers which was neat, but my question is: can we solve this with a short method (using trigonometry)?

Quanto
  • 97,352
Ankit Kumar
  • 311

3 Answers3

3

Hint:

$$-\dfrac14=(\cos(A+B)+\cos(A-B))\cos(A+B)$$

$$\iff\cos^2(A+B)+\cos(A+B)\cos(A-B)+\dfrac14=0$$

which is a Quadratic Equation in $\cos(A+B)$

As $\cos(A+B)$ is real, the discriminant must be $\ge0$

i.e., $\cos^2(A-B)-4\cdot\dfrac14\ge0\iff\sin^2(A-B)\le0$

$\implies\sin(A-B)=0\implies A-B=n\pi$

But for the given ranges of $A,B;$ $$0<A-B<\pi\implies n=0$$

lab bhattacharjee
  • 274,582
2

As you did, rewrite the equation $\cos a\cos b\cos(a+b) = -\frac18$ as

$$f(a,b)=\cos(2a)+\cos(2b)+\cos(2a+2b)= -\frac32$$

By examining $f_a’=f_b’=0$, it can be shown that $f(a,b)\ge -\frac32$; hence the solutions coincide with the minima at $$a=b+ n_1\pi =\pm \frac\pi3+n_2\pi$$

Given the domain restriction $0 < a,b < \frac\pi2$, the only valid solution is $$a=b=\frac\pi3$$

Quanto
  • 97,352
1

Hint:

$$\cos a \cos b \cos (a+b)=\cos^2 a\cos^2 b\cdot(1-\tan a \tan b)=-\frac18$$

hence if $AB=\lambda<0 \iff A>0, B<0$ or $A<0, B>0$,

$$1-\tan a \tan b<0\iff \tan a \tan b>1$$ being $\cos^2 a\cos^2 b>0$ in $0 < a,b < \pi/2$ and $\cos a\cos b\neq 0$, $0 < a,b < \pi/2$.

Sebastiano
  • 7,649