0

Considering my answer for the question Solve $\cos(a)\cos(b)\cos(a+b) = -1/8$ for $0 < a,b < \pi/2$ I have thought to put

$$x=\tan(a), \quad y=\tan(b)$$

in the inequality

$$\tan (a)\cdot \tan (b)>1 \tag 1$$

I will have

$$xy>1 \tag 2$$

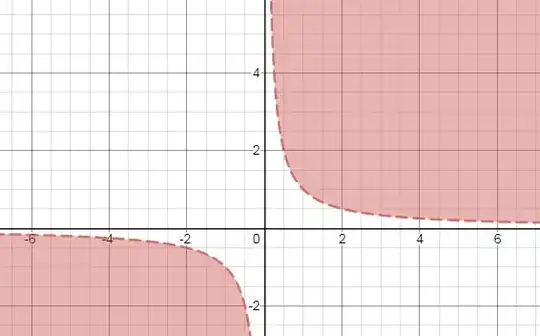
that the $(2)$ it is an equilateral hyperbola when $xy=1$. The crop zone done with Desmos is:

enter image description here

How can I find $a=b=\frac\pi3$?

Using instead Wolfram Alfa I will have many steps https://www.wolframalpha.com/input/?i=%5Ctan+%28a%29%5Ctan+%28b%29%3E1

Is it possible to find with my approach

$$a=b=\frac\pi3\quad ?$$

Sebastiano
  • 7,649
  • 1
    $f(a,b)=\cos a \cos b\cos (a+b)$ has a global minimum $-1/8$ at $a=b=\pi/3$ that's why the equation $\cos a \cos b\cos (a+b)=-1/8$ can be solved so easily. If we try to solve $\cos a \cos b\cos (a+b)=1/2$ we can't, because there are two unknowns. – Raffaele Dec 23 '20 at 21:57
  • @Raffaele :-) Hi from Sicily...Just it is a function of 2 variables. I can calculate $\nabla f=0$ and I think that I can to find the solutions. – Sebastiano Dec 23 '20 at 22:01

2 Answers2

1

First of all, we need both $\tan A,\tan B$ of the same sign

If both are $>0,$ which is true in the given range,

$$\tan A>\cot B=\tan(\pi/2-B)$$

As $\tan(x) $ is increasing in the given range of $A,B$ we need $$A>\pi/2-B$$

We find $$-8(1-xy)=(x^2+1)(y^2+1)$$

$$\iff(x-y)^2+(xy-3)^2=0$$

Can you take it from here?

lab bhattacharjee
  • 274,582
  • Fantastic :-) you and the other user had given the same answer in the same time. – Sebastiano Dec 23 '20 at 20:53
  • But, please, how I find the values $A=B=\pi/3$? – Sebastiano Dec 23 '20 at 20:54
  • 1
    @Sebastiano, Please find the updated version – lab bhattacharjee Dec 23 '20 at 21:02
  • Just starting from the initial equation of the question :-( hence. I can thought $(x-y)^2+(xy-3)^2=0$ like a 2nd equation of in $x$ o in $y$. But $(x-y)^2+(xy-3)^2=0$ give $a=b=\pi/3$? I am curious :-( Can you complete your answer, please? – Sebastiano Dec 23 '20 at 21:09
  • 1
    @Sebastiano, condition $(x-y)^2 + (xy - 3)^2 = 0$ is equivalent to the conditions "$x=y$ and $xy=3$". Hence it's needed to solve the system of two equations $\tan a = \tan b$ and $\tan a \tan b = 3$. From the first one we get that $a=b$ and with the help of the second one we get that $\tan a = \tan b = \sqrt{3}$ and hence $a = b = \frac{\pi}3$. Is there any questions? – Botnakov N. Dec 23 '20 at 21:41
  • @BotnakovN. It is true...:-(...No no..I have understood...What answer must I accept, then? :-( – Sebastiano Dec 23 '20 at 21:45
  • 1
    @Sebastiano, it's not very important. Lab bhattacharjee mentioned that $-8(1-xy)=(x^2+1)(y^2+1)$ iff $(x-y)^2+(xy-3)^2=0$ so it's better to accept his answer. – Botnakov N. Dec 23 '20 at 21:53
1

We have $$\tan a > \frac{1}{\tan b} = \cot b = \tan (\frac{\pi}2 - b),$$ hence $a > \frac{\pi}2 - b$ and $a+b > \frac{\pi}2$.

Botnakov N.
  • 5,660
  • Thank you very much...:-)...upvoted either answers. But why $a=b=\frac\pi3$? – Sebastiano Dec 23 '20 at 20:55
  • 1
    In math.stackexchange.com/questions/3959623 you got that $\tan a \tan b = 1 + \frac{1}{8 \cos^2a \cos^2b }$. The corollary of this relation is $\tan a \tan b > 1$. We showed that the condition $\tan a \tan b > 1$ is equivalent to the condition $ a + b > \frac{\pi}2$. So this corollary doesn't help us to get the answer in the original problem: it gives only necessary condition. – Botnakov N. Dec 23 '20 at 21:06
  • I not know this $\tan a \tan b = 1 + \frac{1}{8 \cos^2a \cos^2b }$! I'm sorry. – Sebastiano Dec 23 '20 at 21:10
  • @Sebastiano, in math.stackexchange.com/questions/3959623 you wrote that $\cos a \cos b \cos (a+b)=\cos^2 a\cos^2 b\cdot(1-\tan a \tan b)=-\frac18$. It follows that $\tan a \tan b = 1 + \frac{1}{8 \cos^2 a \cos^2 b}$. I spoke about it. – Botnakov N. Dec 23 '20 at 21:23
  • Ah. I had not understood. Excuse me. – Sebastiano Dec 23 '20 at 21:24