Rational Function approximation of tan

Question

I wanted to approximate $\tan(x)$ as a rational function by capturing the zero at integer multiples of $\pi$ and poles at odd integer multiples of $\pi$. For convenience, I will be dealing with $\tan(\frac{\pi x}{2})$

$$\tan(\frac{\pi x}{2}) \approx \frac{x}{x^2-1} $$

Now I will shift and sum this approximation for every even integer (where the zeros are - truncated)

Now I will multiply it by the constant $\frac{2}{\pi}$

I check the convergence away from the origin, seems to work

My question is: What is it that I'm doing here? There seems to be some validity to it. It might be converging for the whole complex plane.

Answer 1

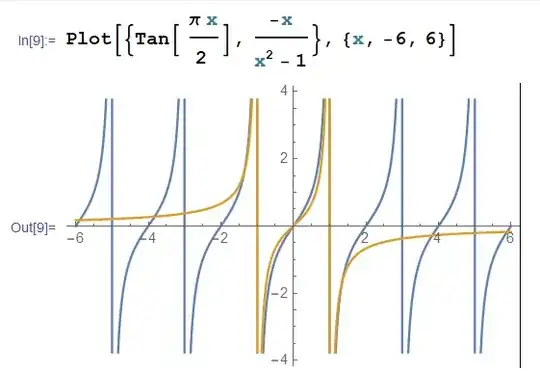
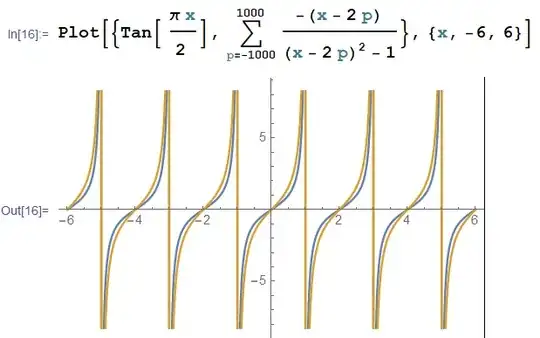
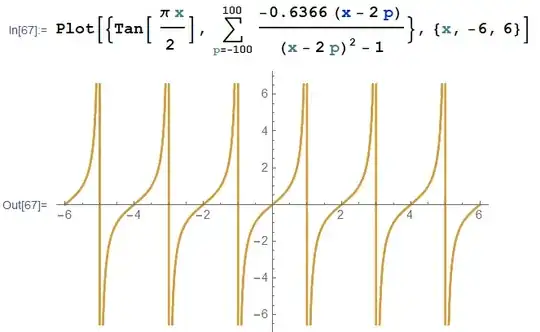
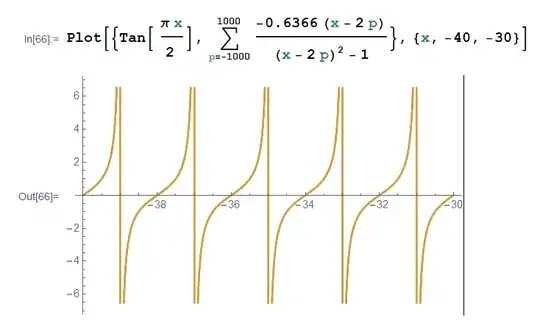
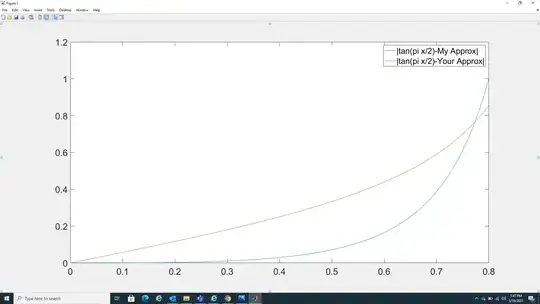
Assuming that you want a rational approximation of $\tan(x)$ for the range $$(2n-1)\frac \pi 2 \leq x \leq (2n+1)\frac \pi 2$$ you could notice that the function $$g(x)=\Big[x-(2n-1)\frac \pi 2\Big]\Big[(2n+1)\frac \pi 2-x\Big]\tan(x)$$ is quite nice since the left and right asymptotes have been removed.

Now, we can build around $x=n \pi$ the Padé approximant of $g(x)$. Using the simple $[3,2]$ would give $$\tan(x)\sim h(x)=\frac{3(n\pi-x)\Big[ \alpha +\beta (x-n\pi)^2\Big] }{\Big[x-(2n-1)\frac \pi 2\Big]\Big[(2n+1)\frac \pi 2-x\Big]\Big[\gamma+\delta (x-n\pi)^2 \Big]}$$ with $$\alpha=15 \pi ^2 \left(12-\pi ^2\right)\qquad \qquad \beta=-720+60 \pi ^2+\pi ^4$$ $$\gamma=-180 \left(12-\pi ^2\right)\qquad \qquad \delta=72 \left(10-\pi ^2\right)$$

For illustration, using $\epsilon=\frac \pi{100}$

$$\int_{0}^{\frac \pi 2-\epsilon} \Big[h(x)-\tan(x)\Big]^2\,dx=5.49\times 10^{-6}$$ corresponding to a relative error of $0.025$%.

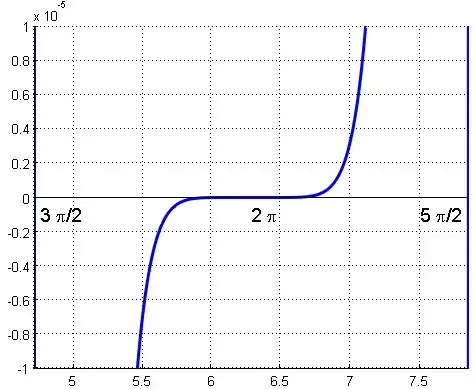
Fig. 1: Representation of the difference $y=h(x)-\tan(x)$ for $n=2$ showing that in the two-thirds of interval $(\frac32 \pi,\frac52 \pi)$, the absolute value of this difference is less than $10^{-5}$.

We can do much better.

Edit

If we use the next approximation of $g(x)$, that is to say its $[5,4]$ Padé approximant, we have $$g(x)= -\frac{\pi^2}4(n\pi-x)\frac {1+a_1(n\pi-x)^2+a_2(n\pi-x)^4 } {1+b_1(n\pi-x)^2+b_2(n\pi-x)^4 }$$ with $$a_1=-\frac{60480-5040 \pi ^2-120 \pi ^4+\pi ^6}{9 \pi ^2 \left(1680-180 \pi ^2+\pi^4\right)}\qquad \qquad a_2=\frac{604800-65520 \pi ^2+420 \pi ^4+\pi ^6}{945 \pi ^2 \left(1680-180 \pi ^2+\pi^4\right)}$$ $$b_1=-\frac{4 \left(1620-174 \pi ^2+\pi ^4\right)}{9 \left(1680-180 \pi ^2+\pi ^4\right)}\qquad \qquad b_2=\frac{1008-112 \pi ^2+\pi ^4}{63 \left(1680-180 \pi ^2+\pi ^4\right)}$$ For this case $$\int_{0}^{\frac \pi 2-\epsilon} \Big[h(x)-\tan(x)\Big]^2\,dx=8.36\times 10^{-12}$$

The plot @Jean Marie kindly added would show that, in the two-thirds of interval $(\frac32 \pi,\frac52 \pi)$, the absolute value of the difference is less than $10^{-8}$.

Answer 2

In https://en.wikipedia.org/wiki/Trigonometric_functions#Partial_fraction_expansion, there is this:

$$\pi \tan(\pi x) =2x\sum_{n=0}^{\infty} \dfrac1{(n+\frac12)^2-x^2} $$

which is similar to yours.

The reference is

Aigner, Martin; Ziegler, Günter M. (2000). Proofs from THE BOOK (Second ed.). Springer-Verlag. p. 149. ISBN 978-3-642-00855-9. Archived from the original on 2014-03-08.

A little more searching (for "partial fraction expansion of tan") led to a proof in https://en.wikipedia.org/wiki/Partial_fractions_in_complex_analysis

Answer 3

Note that $$\frac x{1-x^2}= \tfrac12 \left(\frac1{-1-x} + \frac1{1-x}\right).$$ Therefore your partial sums can be rewritten as $$\tfrac12 \sum_{k=0}^{2N}\left( \frac1{-(2k+1)-x} + \frac1{2k+1-x}\right) = \sum_{k=0}^{2N}\frac x{(2k+1)^2-x^2}. $$ This shows that the limit $N\to \infty$ exists for all $x$ except the odd integers since the summand is $O(k^{-2})$. Then see the answer of Marty and this wikipedia page, that shows some more identities of this nature.

Answer 4

Use the formula: $tan(2x) = \frac{2 \times tan(x)}{1-tan^2(x)}$:
$tan(2 \frac{\pi}{4} x) = \frac{-2 \times tan(\frac{\pi}{4} x)}{tan^2(\frac{\pi}{4} x)-1}$.

So if u use the approximation: $tan(\frac{\pi x}{4}) \approx \frac{\pi x}{4}$ (first term in Taylor series): $tan(2 \frac{\pi}{4} x) = \frac{-2 \times (\frac{\pi}{4} x)}{(\frac{\pi}{4} x)^2-1}$.

Close to what u have written/used. It works well for $0 \leq x \leq 0.8$ but doesnt work well for $x > 0.8 $: See the plot :

Answer 5

The coefficients from other answer didn’t work for me at all. Here’s what worked.

$$f(x) = x \frac{ \frac 1{945} x^4 - \frac 1 9 x^2 + 1 } { \frac 1 {63} x^4 - \frac 4 9 x^2 + 1}$$

I have no idea where the magic numbers coming from, maple printed that in response to pade(tan(x),x,[5,4]). The approximation seems good enough for my use case.