The domino curve

Question

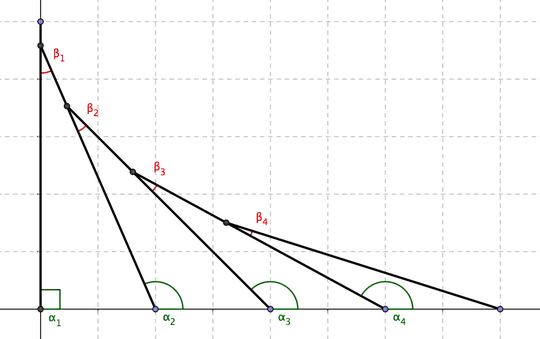
Consider a set of domino tiles with zero thickness evenly spaced apart. Now let them fall but hold the last one upright. The arangement could now look like this:

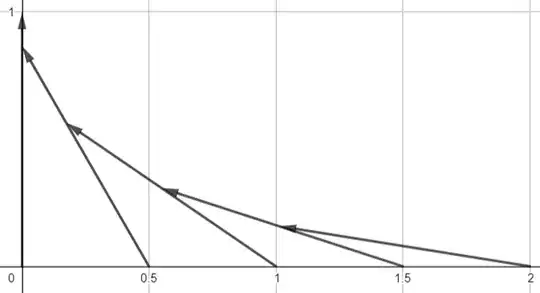
Call the distance between two tiles $d$ and the coordinates of the top of each domino $(p_n,q_n)$, so the $n$-th tile is described by $y_n=\frac{q_n(nd-x)}{nd-p_n}$. However, these equations get complicated fast:

$$y_1 = \sqrt{1-d^2}\left(1-\frac{x}{d}\right) \qquad y_2 = \frac{ \sqrt{1-d^2} \left( d^2 - \sqrt{d^4-d^2+1} \right) (2d-x)}{d \left( d^2 - \sqrt{d^4-d^2+1} -1 \right)}$$

• Is there an easy formula for $(p_n,q_n)$?

Since they all have the same length and are equally spaced it might be easier to look at it from a point-slope perspective. I obtained $(p_n,q_n)$ by finding the intercept between $y_{n-1}$ and $y=\sqrt{1-(x-nd)}$. Maybe there is also a nice representation for the angle at the bottom of the $n$-th tile (depending on $d$) but I wasn't able to find it.

• What curve are all dominoes tangent to?

This also depends on $d$ and if it's too hard, consider only the case $\lim_\limits{d \to 0}$. Such a function would have the following properties:

$$\lim_\limits{x \to \infty} f(x) = \lim_\limits{x \to \infty} f'(x) = 0 \qquad \lim_\limits{x \to 0^+} f(x) = 1 \qquad \lim_\limits{x \to 0^+} f'(x) = -\infty$$

Thanks in advance.

Answer 1

Let $\alpha_k$ and $\beta_k$ be the angles shown below ($\alpha_1=\pi/2$). From the sine rule one gets: $\sin\beta_k=d\sin\alpha_k$. In addition we also have $\alpha_{k+1}=\alpha_k+\beta_k$, which leads to a recursion for $\sin\alpha_k$: $$ \sin\alpha_{k+1}=\sin\alpha_k \left(\sqrt{1-d^2\sin^2\alpha_k}-d\sqrt{1-\sin^2\alpha_k}\right) $$ The coordinates $(p_k,q_k)$ of the vertex of $\beta_k$ can then be expressed as a function of $\sin\alpha_k$: $$ q_k=\sin\alpha_{k+1},\quad p_k=kd+\cos\alpha_{k+1}=kd-\sqrt{1-\sin^2\alpha_{k+1}}. $$