5

Let's start with a few references to get an idea:

Interesting related issues:

Let the length of the blocks on the stack be two ($= 2$ in a certain physical unit) . Assume that each block has a mass equal to one ($= 1$ in a certain physical unit) . Then the center of gravity of a single block is given by: $Z_1 = 1$ . Suppose the center of gravity of the first $(n)$ blocks is given by $Z_n$ , then add one block and find the new center of gravity $Z_{n+1}$ . Place the new block with its left side underneath the old blocks, such that they cannot collapse, i.e. left side exactly at $Z_n$ . $Z_{n+1}$ is given by the mass of the previous $(n)$ blocks times the old center of gravity, plus a distance equal to the old center of gravity (so that the blocks will not collapse), plus one times one (= center of gravity of the newly added block times its mass). The whole must be devided by the new number of blocks. Hence the formula becomes: $$ Z_{n+1} = (n.Z_n + Z_n + 1)/(n+1) \quad \Longrightarrow \quad Z_{n+1} = Z_n + \frac{1}{n+1} $$ Starting with $n = 0$ and $Z_0 = 0$ this becomes: $$ Z_1 = 1 \; , \; Z_2 = 1 + 1/2 \; , \; Z_3 = 1 + 1/2 + 1/3 \; , \; Z_4 = 1 + 1/2 + 1/3 + 1/4 \; , \; \cdots $$ which is precisely the Harmonic Series. Where $Z_4 = 25/12$ and subsequent terms $> 2$ (= length of single block), yet the whole thing doesn't collapse. But what we are really looking for is a continuous approximation of the Harmonic Cantilever. $$ \begin{array}{ll} y = 0 & x = 0 \\ y = -1 & x = 1 \\ y = -2 & x = 1 + 1/2 \\ y = -3 & x = 1 + 1/2 + 1/3 \\ y = -4 & x = 1 + 1/2 + 1/3 + 1/5 \\ ...........&................................ \\ y = -n & x = 1 + 1/2 + 1/3 + ... + 1/n \\ y = -(n+1) & x = 1 + 1/2 + 1/3 + ... + 1/n + 1/(n+1) \end{array} $$ It is seen that $\;y(n+1) - y(n) = [ x(n+1) - x(n) ]\, y(n+1)$ .
For large $(n)$ , the finite differences $[ x(n+1) - x(n) ]$ become smaller and smaller and the quotient $[ y(n+1) - y(n) ] / [ x(n+1) - x(n) ]$ is an approximation of the differential quotient $dy/dx$ . Hence $dy/dx = y$ .
The solution of this differential equation is: $\;y = c \cdot \exp(x)$ . From the above table, we read that $c < 0$ . A kind of best fit between the stack of bricks in the Harmonic Cantilever and this function has been used to determine the constant $(c)$ . A least squares minimalization procedure has been used for this purpose: $$ \sum_{k=1}^N \left[\; y_k - c e^{x_k}\; \right]^2 = \mbox{minimum}(c) $$ Differentiating to $(c)$ and equating the result to zero then results in: $$ c = \frac{\sum_{k=1}^N y_k.e^{x_k}}{\sum_{k=1}^N e^{2\,x_k}} $$ Where $y_k = -1, -2, -3, .. , -N$ . And $x_k = 1 \, ,\, 1 + 1/2 \, ,\, 1 + 1/2 + 1/3 \, ,\, \cdots \, ,\, 1 + 1/2 + 1/3 + .. + 1/N $
Here is the program that calculates the constant: 

program LS;

function konstante : double;
{
  Least Squared Best Fit
}
const
  N : integer = 10000000;
var
  y : integer;
  x,u,v,p : double;
begin
  x := 0;
  u := 0; v := 0;
  for y := 1 to N do
  begin
    p := exp(x);
    x := x + 1/y;
    u := u + yp;
    v := v + pp;
  end;
  konstante := u/v;
end;

begin
  Writeln('|c| =',konstante);
end.
Output (absolute value) : 
|c| = 0.561459525677516
The result is shown in the following picture, for 50 bricks. Two best fit exponential functions are displayed in $\color{red}{red}$ . The best fit exponential function on the right can be formed from the best fit exponential function on the left by translating the latter over a distance of two: $c\,\exp(x) \; \to \; c\,\exp(x-2)$ . So attention may be restricted to the leftmost exponential.

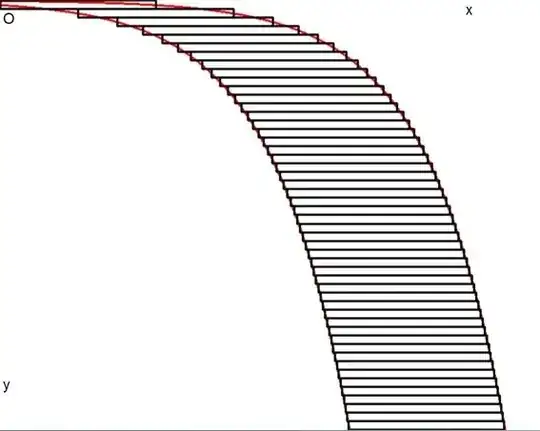
enter image description here

So far so good: we have a numerical approximation for the best fit constant in the exponential function (on the left). But the question is: can the constant $c$ in the conjectured best fit function be determined exactly ?

Han de Bruijn
  • 17,070

1 Answers1

0

Write as follows: $$ - y = - c\cdot e^x = e^{-G} e^x = e^{x-G} $$ Take the logarithm at both sides and specify for values $\,y=-n$ : $$ \ln(-y) = x-G \quad \Longleftrightarrow \quad \ln(n) = \sum_{k=1}^n \frac{1}{k} - G $$ This especially remains valid for very large values of $\,n$ . In the limit: $$ G = \lim_{n \to \infty} \left[ \sum_{k=1}^n \frac{1}{k} - \ln(n) \right] = \gamma $$ Herewith it is proved that $\; |c| = e^{-\gamma}$ , where $\,\gamma\,$ is the Euler–Mascheroni constant . The complete solution is (see above picture) : $$ \color{red}{left :} \quad y = - e^{x-\gamma} \qquad ; \qquad y = - e^{x-\gamma-2} \quad \color{red}{: right} $$

Han de Bruijn
  • 17,070